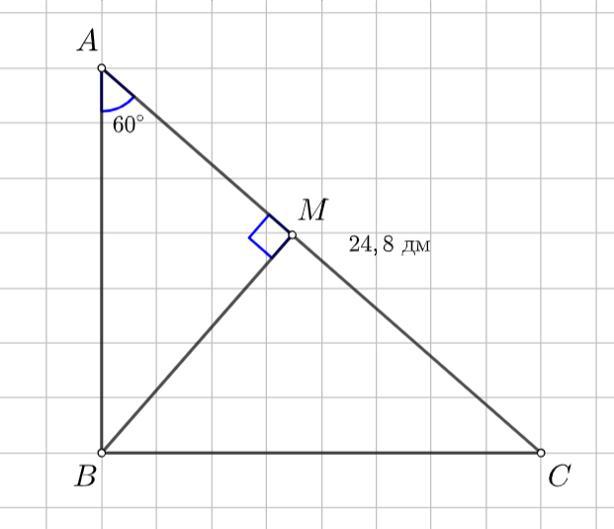
гипотенуза прямоугольного треугольника равна 24.8 дм а один из острых углов равен 60° найдите высоту опущенную из вершины прямого угла на гипотенузу
Ответы
Ответ дал:
2
По метрическим соотношениям в прямоугольном треугольнике, высоту, проведенную к гипотенузе, можно найти по такой формуле:
, где a, b — катеты, с — гипотенуза.
∠BAC = 60°.
Синус острого угла равен отношению противолежащего катета к гипотенузе.
.
Отсюда, (дм).
Поскольку сумма острых углов прямоугольного треугольника равна 90°, то ∠ACB = 90 - 60 = 30°.
В прямоугольном треугольнике напротив угла 30° лежит катет, который равен половине гипотенузы.
Значит, AB = 24,8 : 2 = 12,4 (дм).
Теперь, зная катеты и гипотенузу, найдем высоту треугольника:
(дм).
Ответ: 10,7 дм.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад