Question

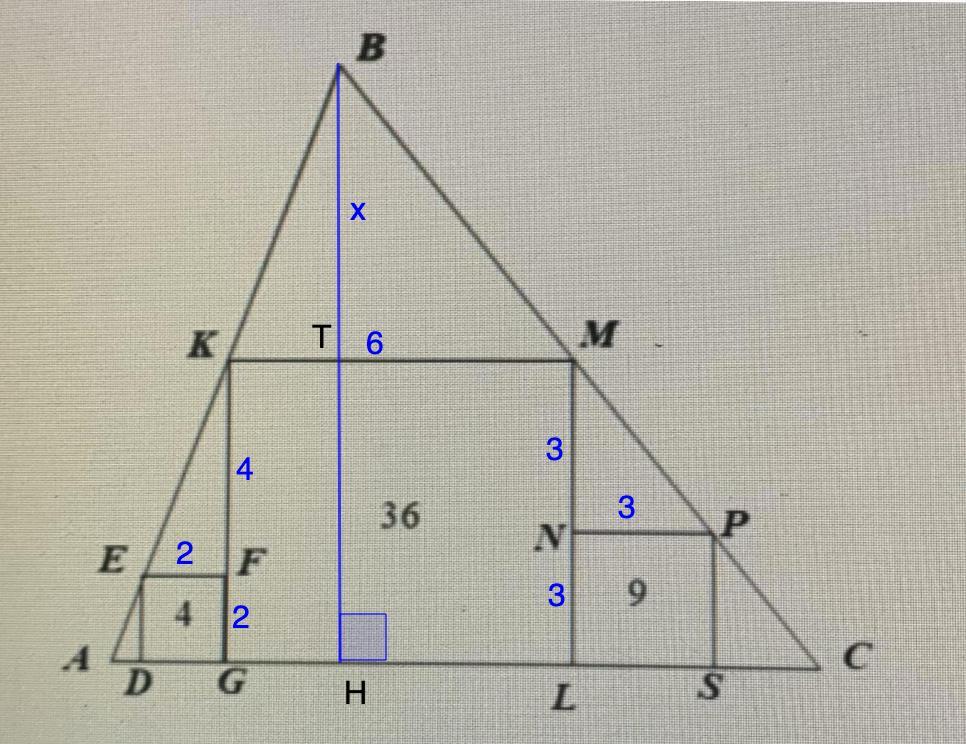
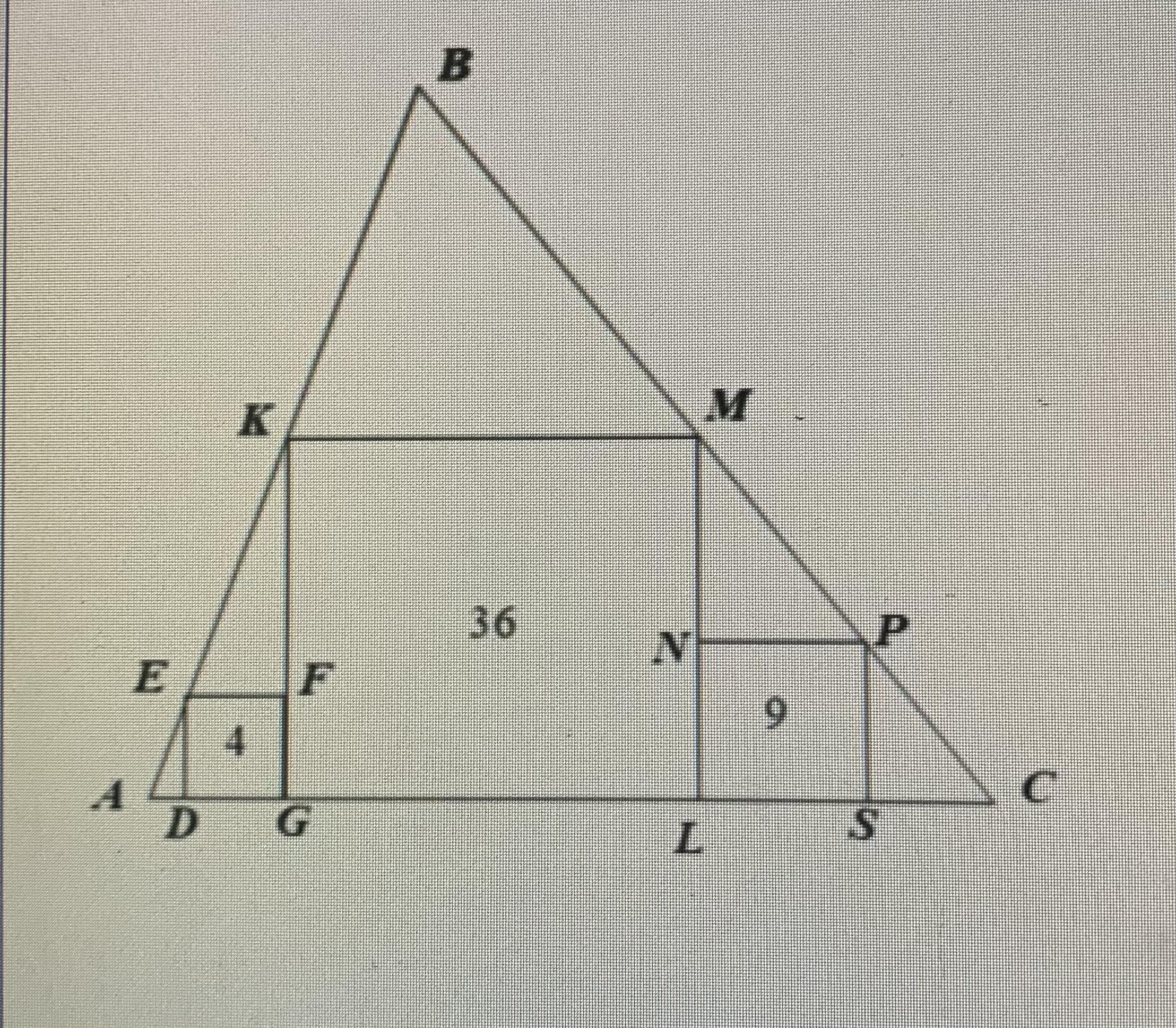
В треугольнике ABC расположено три квадрата DEFG, GKML, LNPS площадью 4,36 и 9 соответственно. Площадь треугольника ABC равна…

Answer 1

Ответ:

Площадь треугольника АВС равна 75 ед.²

Пошаговое объяснение:

Требуется найти площадь треугольника АВС.

Дано: ΔАВС;

DEFG, GKML, LNPS - квадраты.

S(DEFG) = 4, S(GKML) = 36, S(LNPS) = 9.

Найти: S(ABC).

Решение:

1. Найдем стороны квадратов.

• Площадь квадрата равна квадрату его стороны.

S(DEFG) = 4   ⇒   FG = 2,

S(GKML) = 36   ⇒   KG = 6,

S(LNPS) = 9   ⇒   LN = 3.

2. Рассмотрим ΔEKF и ΔAKG - прямоугольные.

EF || AG

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ ΔEKF ~ ΔAKG

KF = 6 - 2 = 4

Запишем отношение сходственных сторон и найдем AG:

$\displaystyle \frac{KF}{KG} =\frac{EF}{AG}\\ \\AG=\frac{KG\cdot{EF}}{KF} =\frac{6\cdot2}{4} =3$

3. Рассмотрим ΔNMP и ΔLMC - прямоугольные.

MP || LC

⇒ ΔNMP ~ ΔLMC (лемма)

MN = 6 - 3 = 3

Запишем отношение сходственных сторон и найдем LC:

$\displaystyle \frac{MN}{ML} =\frac{NP}{LC} \\\\LC=\frac{ML\cdot{NP}}{MN}=\frac{6\cdot3}{3}=6$

4. Найдем АС:

АС = AG + GL + LC = 3 + 6 + 6 = 15

5. Рассмотрим ΔKBM и ΔABC.

KM || AC

⇒ ΔKBM ~ ΔABC

$\displaystyle \frac{KM}{AC} =\frac{6}{15}=k$ , k - коэффициент подобия.

• Площади подобных треугольников относятся как квадрат коэффициента подобия.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

Пусть ВТ = х, тогда ВН = х + 6

$\displaystyle \frac{S(KMB)}{S(ABC)} =k^2\\\\\frac{KM\cdot{TB\cdot2}}{2\cdot{AC}\cdot{BH}} =k^2 \\\\\frac{6x}{15(x+6)}=\frac{6^2}{15^2} \;\;\;\;\;|:\frac{6}{15} \\\\\frac{x}{x+6} =\frac{6}{15}\\ \\15x=6x+36\\\\9x=36\\\\x=4$

⇒ ВН = 4 + 6 = 10

6. Найдем площадь ΔАВС.

$\displaystyle S(ABC)=\frac{1}{2}AC\cdot{BH}=\frac{1}{2}\cdot15\cdot10=75$

Площадь треугольника АВС равна 75 ед.²