Ответы
Ответ дал:
1
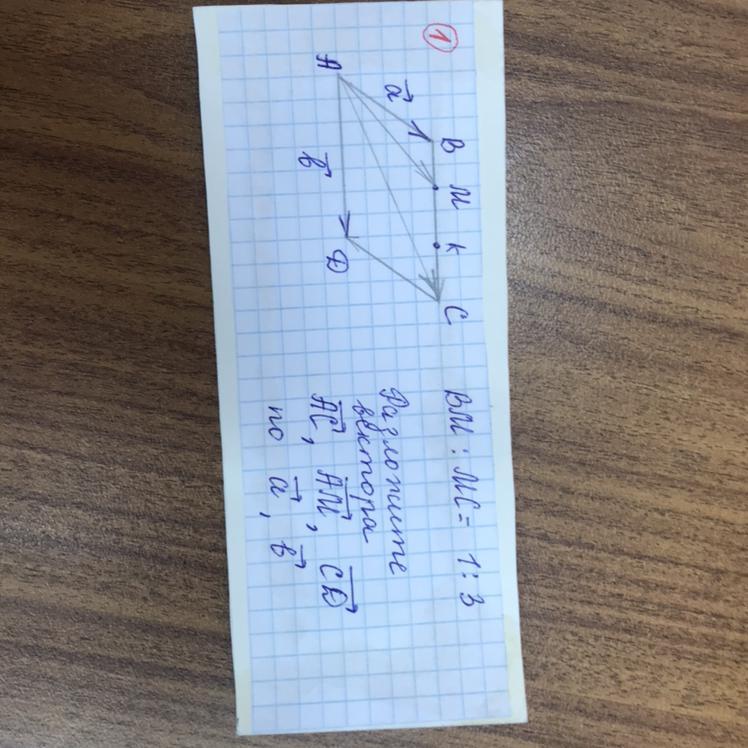
В параллелограмме АВСD , BM:МС=1:3. Вектор АВ равен вектору а, вектор АD равен вектору b. Выразите векторы АС, АМ,СD через вектора
Решение
1) По правилу параллелограмма или
2)По правилу треугольника . По условию на отрезок ВС приходится 1+3=4 части , поэтому
.
Получаем .
3) , тк противоположные ,
zakk5225:
спасибо, можешь еще пожалуйста сам отрезок нарисовать
могу . А какой?
знать бы куда вам фото отправить
кидай здесь . Посмотрю.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад