Ответы
Ответ:
Номер 1
Угол при вершине
<3=180-82•2=16 градусов
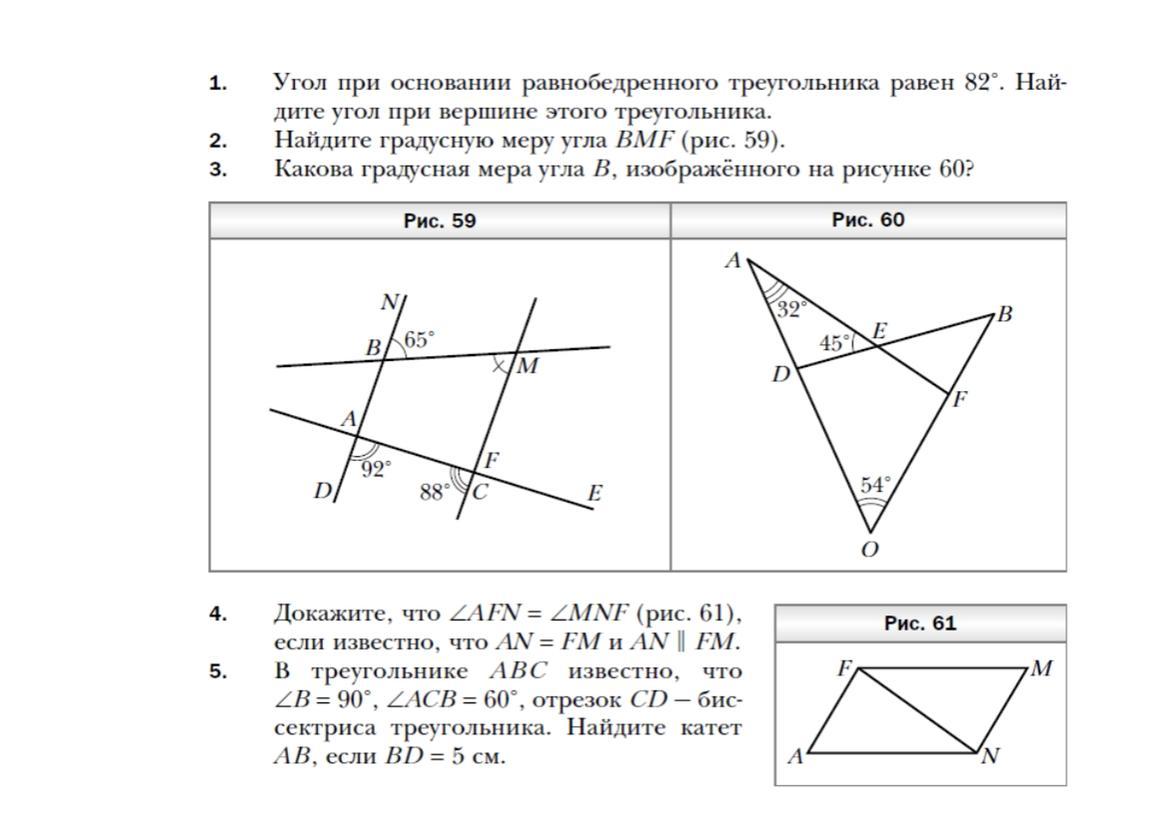
Номер 2
<ВМF=<NBM=65 градусов ,как накрест лежащие при ND || MC и секущей ВМ
Параллельность прямых доказывается так:
<92+<88=180 градусов,как односторонние
Если при пересечении прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
Номер 3
Треугольник АFO
<AFO=180-(32+54)=94 градуса
<АFO+<EFB=180 градусов,как смежные
<ЕFB=180-94=86 градусов
<FEB=<AED=45 градусов,как вертикальные
<В=180-(86+45)=49 градусов
Номер 4
Так как AN || FM,то
<NFM=<ANF,как накрест лежащие при АN || FM и секущей FN
FM=AN, по условию задачи
FN-общая сторона
Треугольники равны по 1 признаку равенства треугольников-по двум сторонам и углу между ними,
а значит равны и соответствующие стороны и соответствующие углы
<АFN=<MNF
Номер 5
Биссектриса разделила прямоугольный треугольник на два треугольника.Один из них так и остался прямоугольным,с катетом DB=5 см,он лежит напротив <DCB=30 градусов т к биссектриса
DC разделила угол С на два равных угла
<DCB=<ACD=60:2=30 градусов
А значит катет DB в два раза меньше гипотенузы DC
DC=5•2=10 см
Теперь рассмотрим второй образовавшийся треугольник АDC
Oн равнобедренный,т к углы при его основании равны по 30 градусов
<АСD=<DAC=30 градусов
(<А в треугольнике АВС=90-60=30 градусов)
А значит
АD=DC=10 cм
АВ=АD+DB=10+5=15 cм
Объяснение: