792. Изобразите множества на кругах Эйлера-Венна: 1) A — множество натуральных чисел, В множество простых чисел; 2) A – множество натуральных чисел, В множество составных чисел; 3) A – множество составных чисел, В множество простых чисел; 4) A – множество простых чисел, В- множество четных чисел.
Ответы
Ответ:
Изобразили множества на кругах Эйлера-Венна.
Пошаговое объяснение:
Требуется изобразить множества на кругах Эйлера-Венна.
- На диаграммах Эйлера множества изображаются кругами.
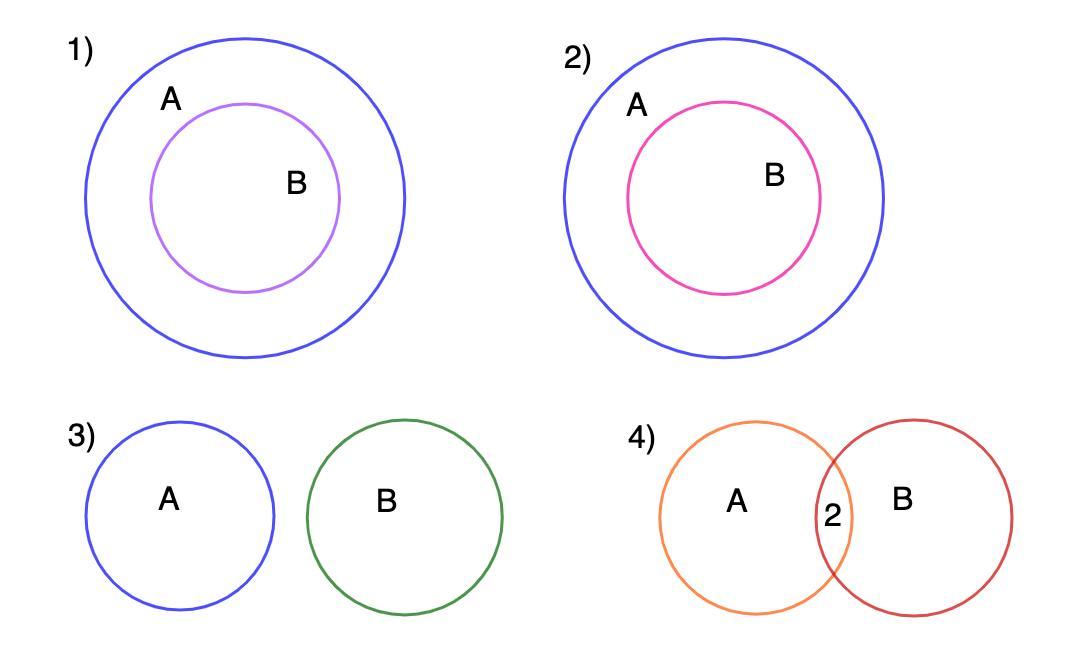
1) A - множество натуральных чисел, В - множество простых чисел;
- Простые числа - это натуральные числа, которые делятся на единицу и на самого себя.
Поэтому множество простых чисел является подмножеством натуральных чисел.
В ⊆ А.
2) A – множество натуральных чисел, В - множество составных чисел;
- Составные числа - это натуральные числа, которые кроме единицы и на само себя, имеют другие делители.
Множество составных чисел также является подмножеством натуральных чисел.
В ⊆ А
3) A – множество составных чисел, В - множество простых чисел;
Данные множества не пересекаются, поэтому изобразим их двумя непересекающимися кругами.
А ∩ В = ∅
4) A – множество простых чисел, В- множество четных чисел.
У данных множеств есть число 2, которое является и простым и четным.
Поэтому эти множества будут пересекаться.
А ∩ В.
См. рисунок