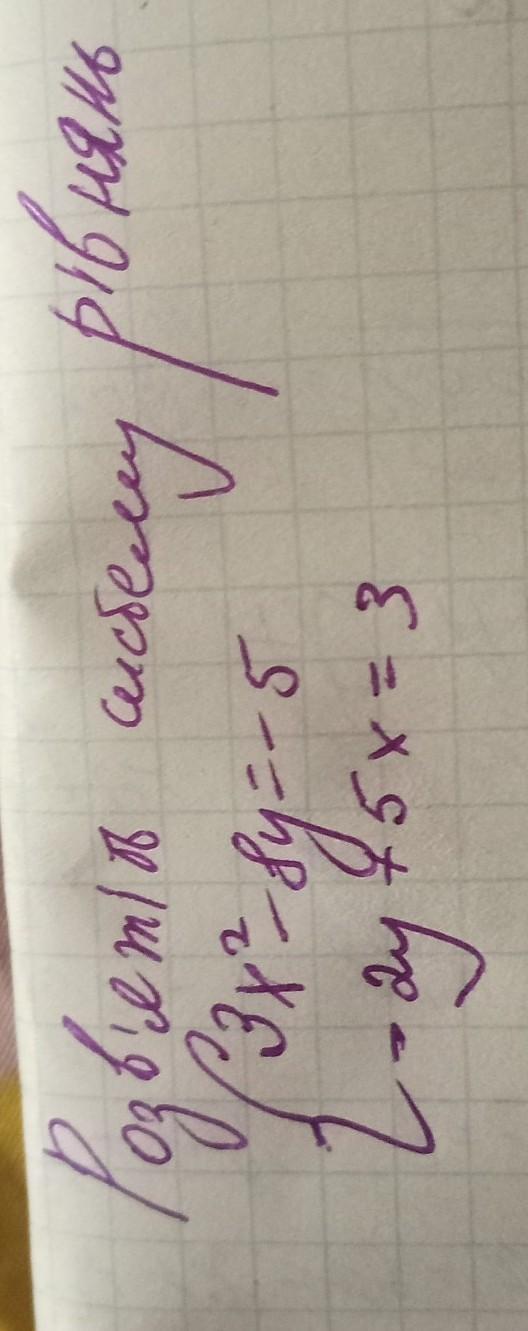Question

допоможіть будь ласка!! дуже треба, дякую ​

Answer 1

Ответ:

В решении.

Объяснение:

Решить систему уравнений:

3х² - 8у = -5

-2у + 5х = 3

Умножить второе уравнение на -4, чтобы применить способ сложения.

Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.

3х² - 8у = -5

8у - 20х = -12

Сложить уравнения:

3х² - 20х - 8у + 8у = -5 - 12

3х² - 20х + 17 = 0, квадратное уравнение, ищем корни:

D=b²-4ac = 400 - 204 = 196        √D=14

х₁=(-b-√D)/2a  

х₁=(20-14)/6

х₁=6/6

х₁= 1;              

х₂=(-b+√D)/2a

х₂=(20+14)/6

х₂=34/6  (деление)

х₂= 17/3 (дробь);

Теперь подставить значение х в любое из двух уравнений системы и вычислить у:

-2у + 5х = 3

-2у = 3 - 5х

2у = 5х - 3

Вычислить у₁:

2у = 5 * 1 - 3

2у = 2

у₁ = 1;

Вычислить у₂:

2у = 5х - 3

2у = 5 * 17/3 - 3

Умножить все части уравнения на 3, чтобы избавиться от дроби:

6у = 85 - 9

6у = 76

у = 76/6  (деление)

у₂ = 38/3 (дробь);

Решения системы уравнений: (1; 1);   (17/3; 38/3).

Проверка путём подстановки  вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.

Answer 2

Ответ:

(x₁; y₁)=(1; 1), (x₂; y₂)=$\bf \bigg(5\dfrac{2}{3} ;~12\dfrac{2}{3} \bigg).$

Объяснение:

• Решение методом подстановки.

$\displaystyle\left \{ {{3x^2-8y=-5} \atop {-2y+5x=3}} \right. \Leftrightarrow \left \{ {{3x^2-8y=-5} \atop {5x=3+2y~\bigg|:5}} \right.\Leftrightarrow \left \{ {{3x^2-8y=-5} \atop {x=\dfrac{3}{5}+\dfrac{2}{5} y }} \right.\Rightarrow \\3\bigg(\frac{3}{5} +\frac{2}{5} y\bigg)^2-8y=-5\Leftrightarrow 3\bigg(0,6+0,4y\bigg)^2-8y+5=0\Leftrightarrow \\3\cdot(0,36+0,48y+0,16y^2)-8y+5=0\Leftrightarrow 1,08+1,44y+0,48y^2-8y+5=0\\\Leftrightarrow 6,08-6,56y+0,48y^2=0\Leftrightarrow 0,48y^2-6,56y+6,08=0$

$\Leftrightarrow D=b^2-4ac=(-6,56)^2-4\cdot 0,48\cdot 6,08=31,36\Leftrightarrow x_{1;2} =\displaystyle\frac{-b\pm\sqrt{D} }{2a} \Leftrightarrow \\x_1=\frac{6,56-5,6}{2\cdot 0,48} =\frac{0,96}{0,96} =1;~x_2=\frac{6,56+5,6}{2\cdot 0,48}=\frac{12,16}{0,96} =\frac{\dfrac{304}{25} }{\dfrac{24}{25} } =\frac{304}{24} =\frac{38}{3} =12\frac{2}{3} .$

Подставляем корни в уравнение $x=\displaystyle\frac{3}{5} +\frac{2}{5} y:\\x_1=\frac{3}{5} +\frac{2}{5}\cdot1=\frac{5}{5} =1;\\x_2=\frac{3}{5} +\frac{2}{5}\cdot\frac{38}{3} =\frac{3}{5} +\frac{76}{15} =\frac{9+75}{15} =\frac{85}{15} =\frac{17}{3} =5\frac{2}{3} .$