Ответы
Ответ дал:
0
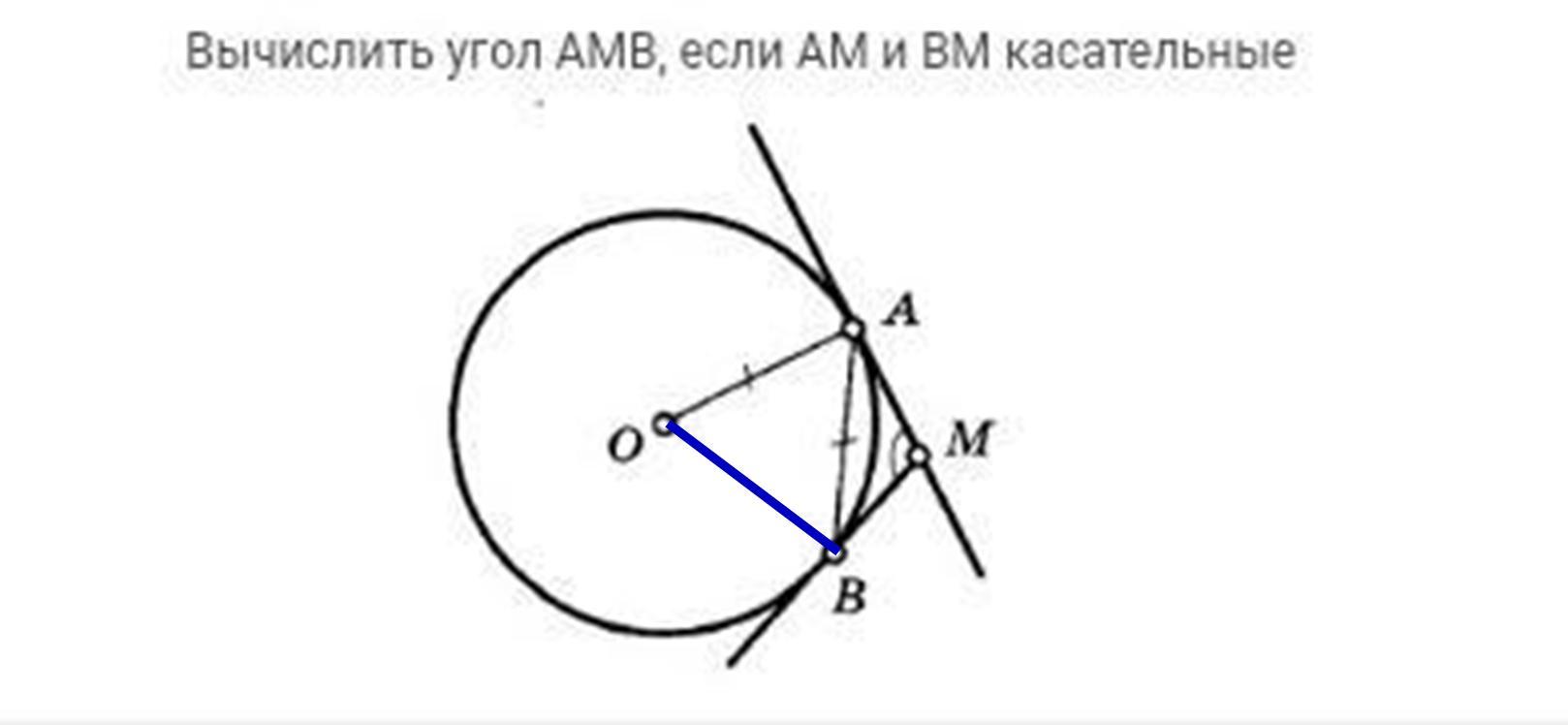
1) АМ и МВ - касательные, значит, ∠ОАМ=∠ОВМ = 90°
2) Проведём радиус ОВ и рассмотрим полученный ΔОАВ.
У него
ОА=АВ - по условию
ОА=ОВ - как радиусы одной окружности.
Если АВ = ОА, а ОА=ОВ, значит, АВ=ОВ.
А если АВ = ОА = ОВ, то это значит, что ΔОАВ - равносторонний.
Тогда ∠АОВ=∠ОАВ=∠АВО = 60°
3) Рассмотрим четырёхугольник ОВМА.
В нём
Зная, что касательная перпендикулярна радиусу окружности, проведённому в точку касания, получаем:
∠ОАМ=∠МВО=90°
∠АОВ=60°
Сумма внутренних углов четырёхугольника равна 360°.
Отсюда ∠АМВ = 360° - (90°+90°+60°)=120°
Ответ: ∠АМВ = 120°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
