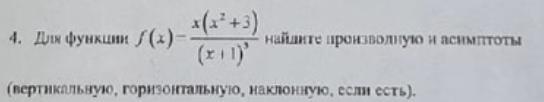Ответы
Ответ дал:
2
Ответ:
b) Вертикальная асимптота х=а, если .
Проверим точку а= -1 , так как при х= -1 функция не существует, знаменатель дроби обращается в ноль .
Вертикальная асимптота х= -1 .
c) Наклонная асимптота y=kx+b .
Получили уравнение горизонтальной асимптоты .
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад