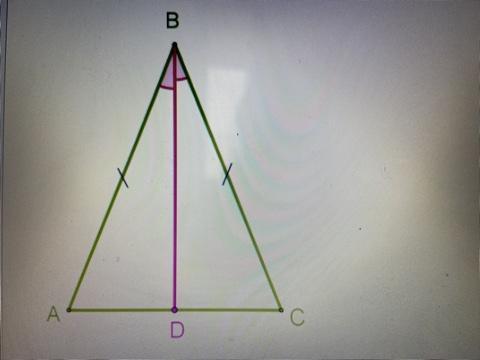
В равнобедренном треугольнике с длиной основания 53 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.
Рассмотрим треугольники ΔABD и Δ ....
(треугольник записать в алфавитном порядке);
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ ....
2. так как проведена биссектриса, то ∡ ....
= ∡ CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — ....
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
AD= .... см
Там где я написала .... там нужно ответ записать
Даю 60 балов
Приложения:
Ответы
Ответ дал:
0
Рассмотрим треугольники ΔABD и Δ ВСD
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ С
2. так как проведена биссектриса, то ∡ АBD= ∡ CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — равнобедренный
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
AD= 53:2=26,5 см
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад