Question

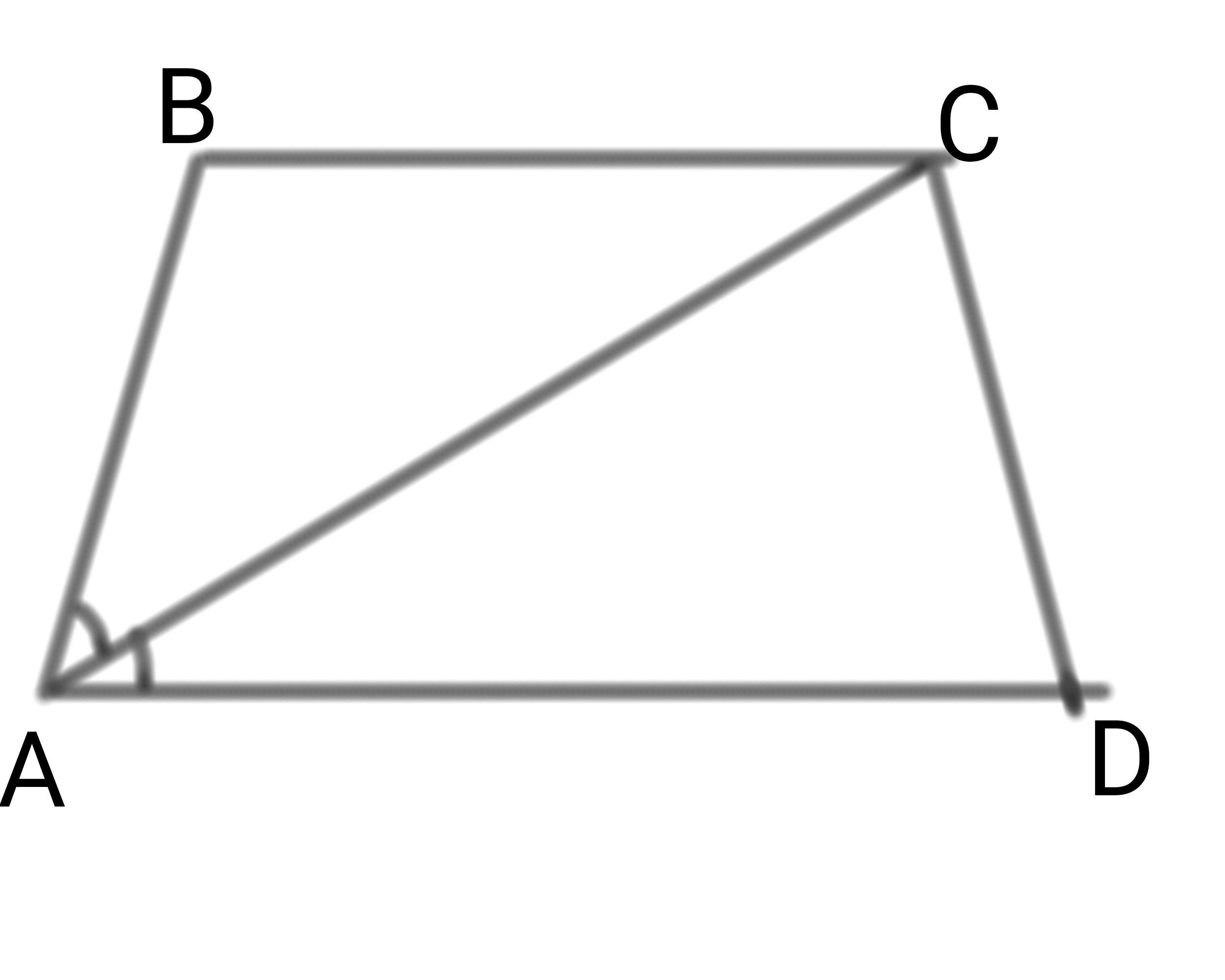
Задана равнобедренная трапеция ABCD. Диагональ AC, равная 6*корень3, является биссектрисой острого угла A = 60°. Найдите периметр трапеции. Пожалуйста.

Answer 1

Ответ:

Трапеция равнобедренная AB=CD.

AC=6√3

∠A=60°

В равнобедренной трапеции прилежащие к боковой стороне углы дают в сумме 180°.

∠B=180°-60°=120°

Диагональ по условию делит острый угол ∠А пополам, значит ∠BAC=30°.

Рассмотрим ΔABC:

Сумма внутренних углов треугольника 180°.

∠ABC+∠BAC+∠ACB=180°

120°+30°+∠ACB=180°

∠ACB=30°

Так как ∠ACB=∠BAC, ΔACB – равнобедренный. Значит боковые стороны и меньшее основание равны, AB=CD=BC.

По теореме синусов, стороны пропорциональны синусам противолежащего угла.

$\frac {AC} { \sin(\angle ABC)}= \frac {AB} { \sin( \angle ACB)}$

$\frac{6 \sqrt{3} }{ \sin( {120}^{ \circ} ) } = \frac{x}{ \sin( {30}^{ \circ} ) }$

$\frac{6}{ \frac{ \sqrt{ 3 } }{2} } = \frac{x}{ \frac{1}{2} } \\ 12 = 2x \\ x = 6$

AB=6

Следовательно, AB=BC=CD=6.

∠B=∠C, потому что это равнобедренная трапеция.

∠ACD=∠C-∠ACB

∠ACD=120°-30°=90°

Значит ΔACD – прямоугольный, где угол ∠ACD – прямой.

По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.

AD²=AC²+CD²

${AD}^{2} = {(6 \sqrt{3}) }^{2} + {6}^{2} \\ {AD}^{2} = 108 + 36 \\ {AD}^{2} = 144 \\ AD = \sqrt{144} \\ AD = 12$

P=AB+BC+CD+AD

P=6+6+6+12=30