Задание 5. На координатной плоскости схематически изобразите графики функций. Укажите их область определения и область значений. (задания на фотке)
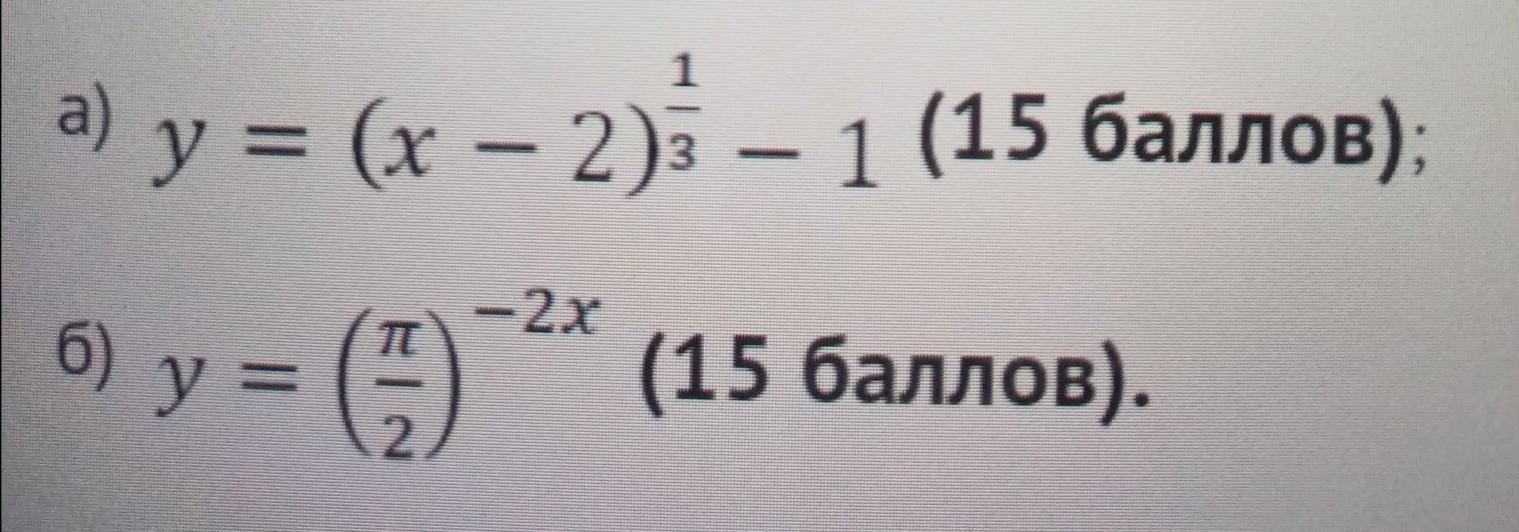
Ответы
Ответ:
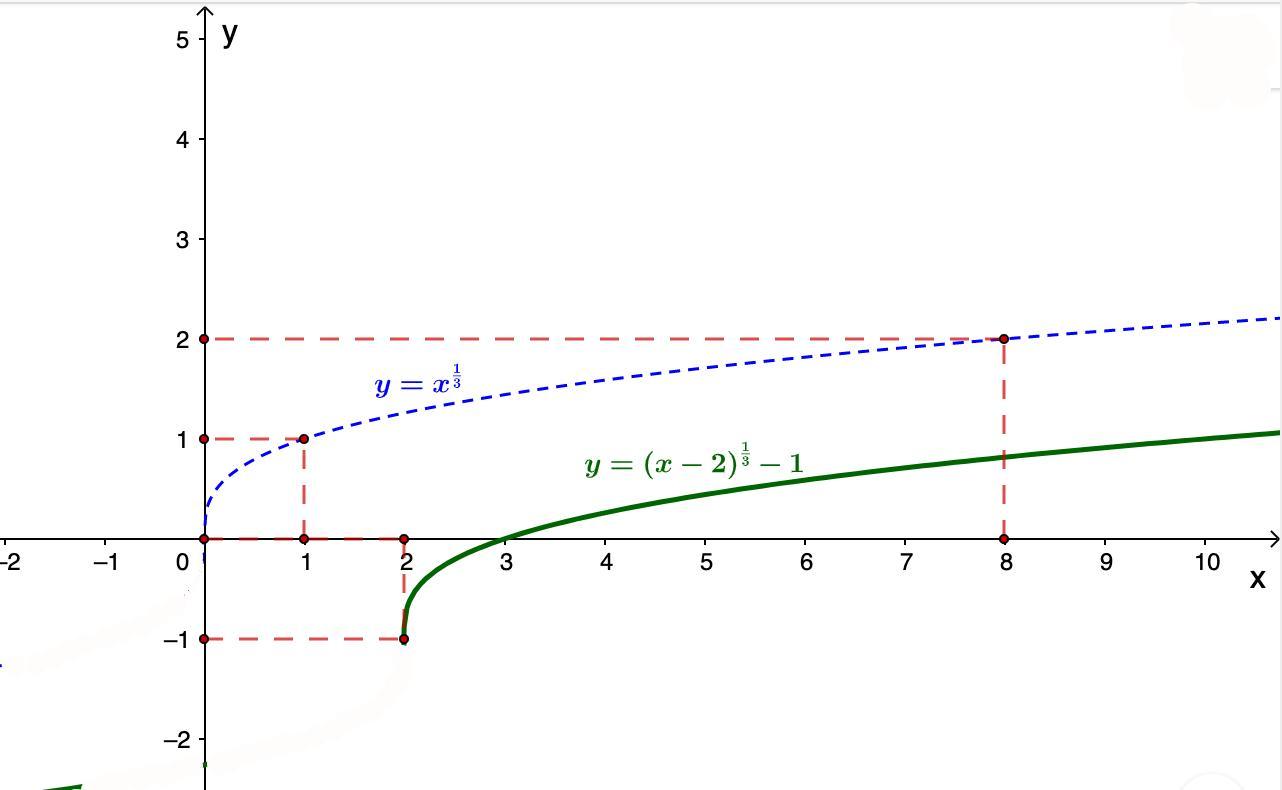
а) Область определения:
D(y): [2; +∞)
Область значений:
Е(y): [-1; +∞)
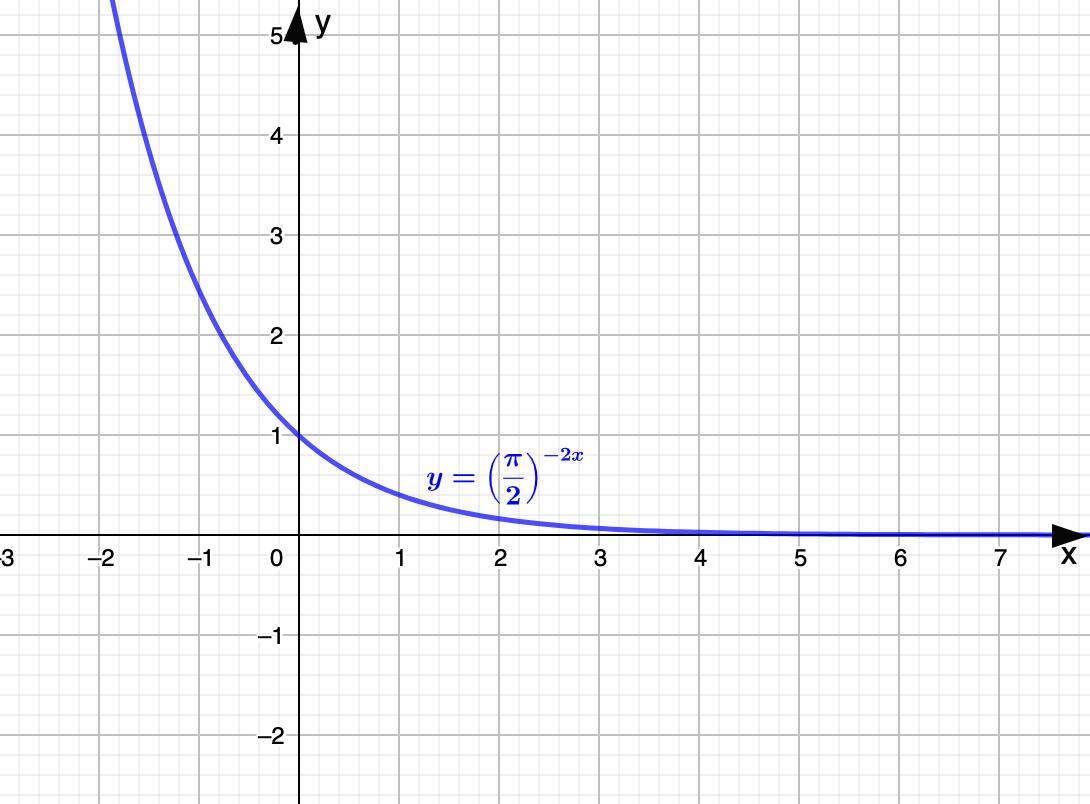
б) Область определения:
D(y): (-∞; +∞)
Область значений:
Е(y): (0; +∞)
Объяснение:
Требуется на координатной плоскости схематически изобразить графики функций. Указать их область определения и область значений.
а)
График этой функции получается из графика путем сдвига на две единица вправо и на одну единицу вниз.
График
- степенная функция с положительным дробным показателем, определена для неотрицательных чисел, то есть х ≥ 0.
Построим график.
х = 0; у = 0;
х = 1; у = 1
х = 8; х = 2
Затем сдвигаем построенный график на две единицы вправо и на одну единицу вниз.
Область определения:
D(y): [-1; +∞)
Область значений:
Е(y): [2; +∞)
б)
- показательная функция.
Если х = 0, то у = 1. Следовательно, график пересекает ось 0у в точке (0; 1)
Так как
и
, то данная функция убывающая.
Вспомним:
- Положительное число в любой степени положительно.
Значит график расположен выше оси 0х, то есть y > 0.
Область определения:
D(y): (-∞; +∞)
Область значений:
Е(y): (0; +∞)