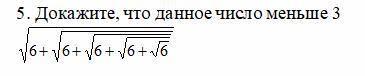Question

Очень срочно нужно (

Answer 1

Ответ:

Доказательство описано ниже.

Пошаговое объяснение:

Докажите, что данное число меньше 3.

Отметим, что для всех положительных чисел a и b из того, что a<b следует, что a²<b² и наоборот. Значит $\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} } } } }$будет меньше 3, если таким же знаком неравенства сравниваются их квадраты, то есть

$\left(\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} } } } }\right )^2 < 3^2$

$6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} } } } < 9\\\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} } } } < 9-6\\\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} } } } < 3$ - это в свою очередь будет верно, если таким же знаком сравниваются квадраты этих чисел:

$\left(\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6} }} } }\right )^2 < 3^2$

Тут уже 4 знака корня. Аналогично переходим к неравенству  

$\left(\sqrt{6+\sqrt{6+\sqrt{6} } }\right )^2 < 3^2$ и так далее продолжаем возводить в квадрат и переносить 6 из левой части в правую, пока не дойдем до неравенства $\left(\sqrt{6}\right )^2 < 3^2$  , равносильного 6<9.

Последнее неравенство верно, а значит, поднимаясь вверх по цепочке получаем, что верны и все неравенства выше, что и требовалось доказать.