Question

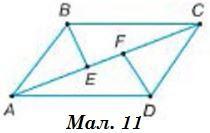
На Мал. 11 АВ = CD, AD = BC, BE і DF – бісектриси кутів В і D.
а) знайдіть кут ВАС, якщо ACD = 35°.

б) знайдіть АЕ, якщо СF = 3 см.

Answer 1

Відповідь: а) ∠BAС = 35°; AE = 3 см.

                                            Пояснення:

Оскільки протилежні сторони чотирикутника ABCD рівні за умовою (АВ = CD, BС =AD), то цей чотирикутник є паралелограмом.

a)

AB = CD; BC = AD. Так як ABCD — паралелограм, то ∠ABC = ∠CDA.

Значить, Δ ABC = ∠ACD за двома сторонами і кутом між ними (першою ознакою рівності).

Звідси, ∠BAС = ∠ACD = 35°.

б)

AB = CD.

BE і DF – бісектриси ∠ABC і ∠CDA, тож вони ділять їх навпіл

Так як ABCD — паралелограм, то ці кути є рівними: ∠ABC = ∠CDA.

Значить, і їх половини також рівні одна одній: ∠ABE = ∠CDF.

∠BAС = ∠ACD (доведення в попередньому пункті).

Отже, Δ ABE  = ∠CDF за стороною і прилеглими до неї кутами (другою ознакою рівності).

Тоді AE = CF = 3 см.