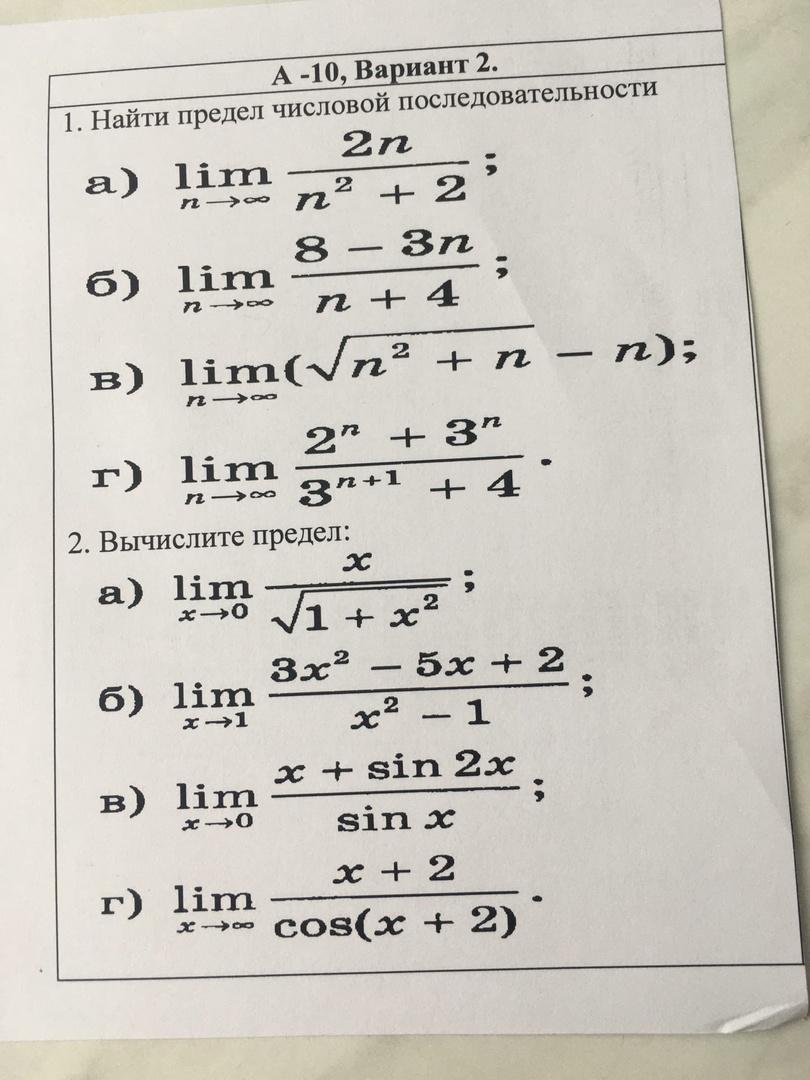Ответы
Ответ дал:
0
Ответ:
1.
а)
б)
в)
г)
2.
а)
б)
в)
г)
Примечание:
- первый замечательный предел
Объяснение:
1.
а)
б)
в)
-------------------------------------------------------------------------------------------------
1)
-------------------------------------------------------------------------------------------------
г)
1)
, а показательная функция
при
и
стремится к нулю.
2.
а)
Пункты номера 2 б), в) и г) смотрите на фотографии!
Приложения:

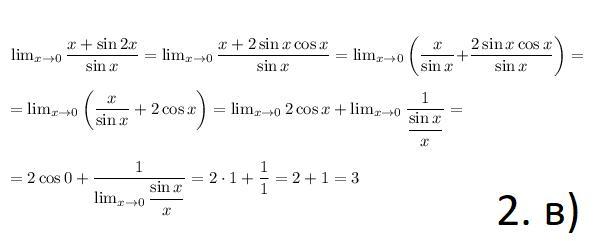


Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад