Question

СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА
100 БАЛЛОВ

см. фото

Answer 1

$\displaystyle\bf\\u(x_{0} )=-3 \ \ ; \ \ u'(x_{0} )=-6\\\\v(x_{0} )=-6 \ \ ; \ \ v'(x_{0} )=-4\\\\f(x)=\frac{u(x)}{v(x)}$

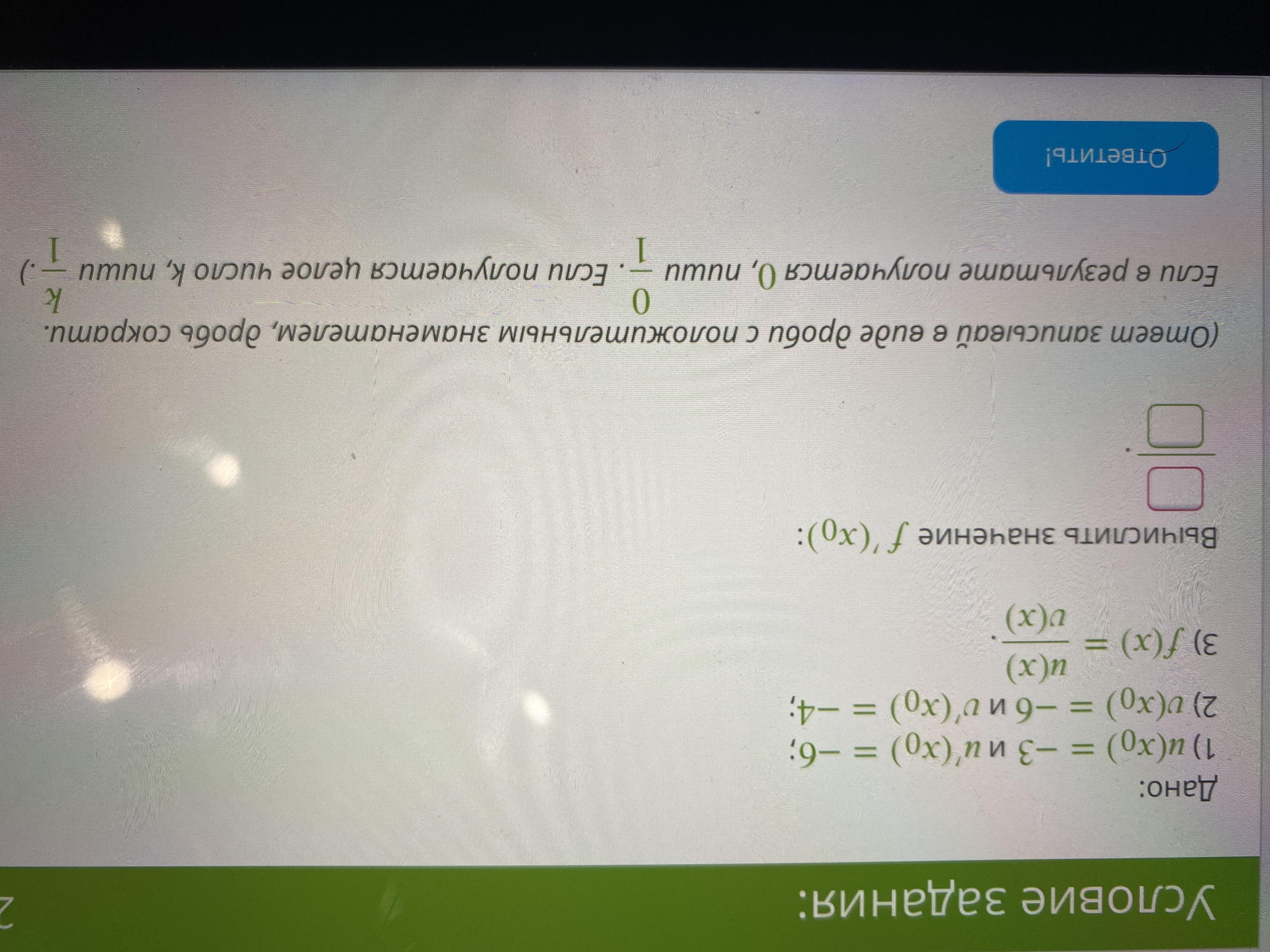
По правилу нахождения производной частного получим :

$\displaystyle\bf\\f'(x)=\frac{u'(x)\cdot v(x)-u(x)\cdot v'(x)}{v^{2}(x) } \\\\\\f'(x_{0} )=\frac{u'(x_{0} )\cdot v(x_{0} )-u(x_{0} )\cdot v'(x_{0} )}{v^{2}(x_{0} ) }$

Подставим данные в условии значения и получим :

$\displaystyle\bf\\f'(x_{0} )=\frac{-6\cdot(-6)-(-3)\cdot(-4)}{(-6)^{2} } =\frac{36-12}{36} =\frac{2}{3} \\\\\\Otvet:\frac{2}{3}$