Question

с решением пожалуйста ​

Answer 1

Ответ:

А) 1

Объяснение:

$\displaystyle \frac{x+3}{x^2-4}-\frac{1}{x+2} < \frac{2x}{2x-x^2};$

$\displaystyle \frac{x+3}{(x-2)(x+2)}-\frac{1}{x+2} -\frac{2x}{x(2-x)} < 0;$

Если х≠0, то

$\displaystyle \frac{x+3-(x-2)}{(x-2)(x+2)}+\frac{2}{x-2} < 0;$

$\displaystyle \frac{x+3-x+2+2(x+2)}{(x-2)(x+2)} < 0;$

$\displaystyle \frac{5+2x+4}{(x-2)(x+2)} < 0;$

$\displaystyle \frac{2x+9}{(x-2)(x+2)} < 0;$

Найдём нули функции:
2x+9=0 ⇒ x = -4,5
x-2 = 0 ⇒ x = 2
x+2 = 0 ⇒ x = -2
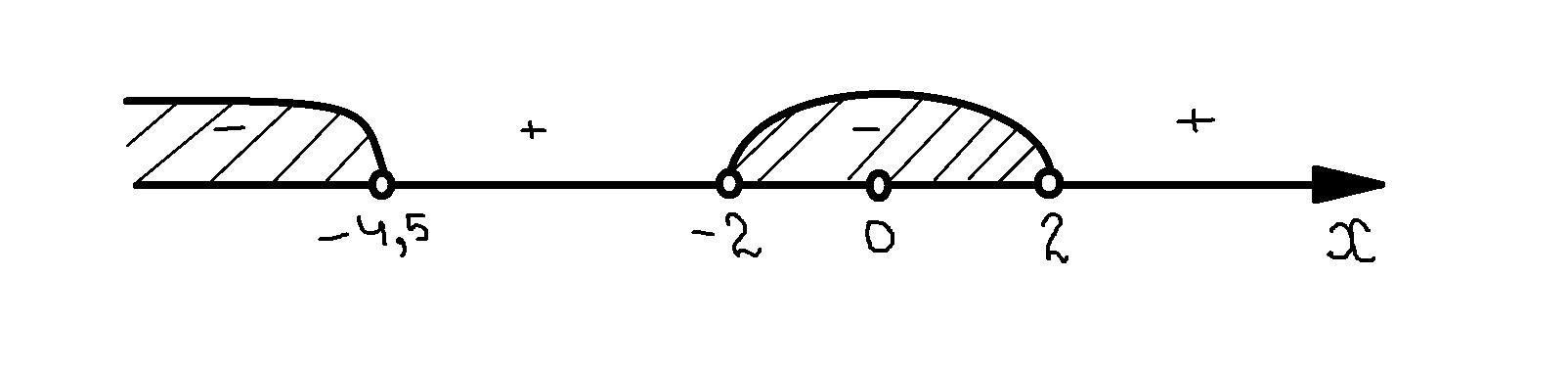
Расположим эти точки на координатной прямой и найдём знак на каждом промежутке(см. вложение)
$\displaystyle y(-5)=\frac{2*(-5)+9}{((-5)-2)((-5)+2)} =\frac{-10+9}{(-7)*(-3)}=-\frac{1}{21}$ (знак отрицательный)

$\displaystyle y(-3)=\frac{2*(-3)+9}{((-3)-2)((-3)+2)} =\frac{-6+9}{(-5)*(-1)}=\frac{3}{5}$ (знак положительный)

$\displaystyle y(0)=\frac{2*0+9}{(0-2)(0+2)} =\frac{9}{(-2)*2}=-\frac{9}{4}$ (знак отрицательный)

$\displaystyle y(3)=\frac{2*3+9}{(3-2)(3+2)} =\frac{6+9}{1*5}=\frac{15}{5}=3$ (знак положительный)
Если сложить решение неравенства и условие задачи, то получается следующая система:

$\displaystyle \left \{ {{\left[\begin{array}{ccc}x < -4,5\\-2 < x < 2\\x\neq 0\end{array}\right } \atop {x\leq 0}} \right. < = > 0 < x < 2$

Единственное целое значение в этом диапазоне равняется 1