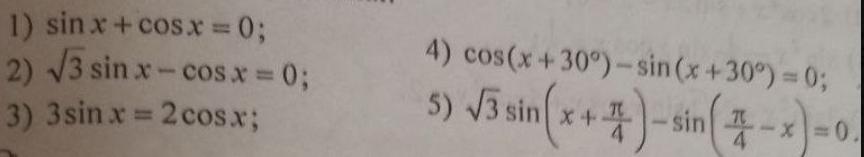Ответы
Ответ:
1) sin(x)+cos(x)=0 |÷cos(x)
tg(x)+1=0
tg(x)= -1
x= -π/4+πk k€Z
2) √(3)*sin(x)-cos(x)=0 |÷cos(x)
√(3)tg(x)= -1
tg(x)= -√(3)/3
x= -π/6+πk k€Z
3) 3sin(x)=2cos(x) |÷cos(x)
3tg(x)=2
tg(x)=2/3
x=arctg(2/3)+πk k€Z
4) cos(x+30°)-sin(x+30°)=0
cos(x+30°)=sin(x+30°)
cos(x)*cos(30°)-sin(x)*sin(30°)=sin(x)*cos(30°)+cos(x)*sin(30°)
√(3)/2*cos(x)-0.5*sin(x)=√(3)/2*sin(x)+0.5*cos(x)
√(3)/2cos(x)-√(3)/2sin(x)=0.5cos(x)+0.5sin(x)
√(3)(cos(x)-sin(x))=cos(x)+sin(x)
(√(3)-1)cos(x)-(√(3)+1)sin(x)=0 |÷(√(3)+1)sin(x)
(√(3)/2-1/2)ctg(x)=1
ctg(x)=1/(√(3)/2-1/2)
x=arcctg(1/(√(3)/2-1/2))+πk k€Z
5)√(3)sin(x+π/4)-sin(π/4-x)=0
√(3)sin(x)*cos(π/4)+√(3)cos(x)*sin(π/4)-sin(π/4)*cos(x)+cos(π/4)*sin(x)=0
√(3/2)sin(x)+√(3/2)cos(x)-√(2)/2*cos(x)+√(2)/2sin(x)=0
делим на √(2)/2*sin(x)
√(3)+√(3)ctg(x)-ctg(x)+1=0
ctg(x)=(√(3)+1)/(√(3)-1)
x=arcctg((√(3)+1)/(√(3)-1))+πk k€Z