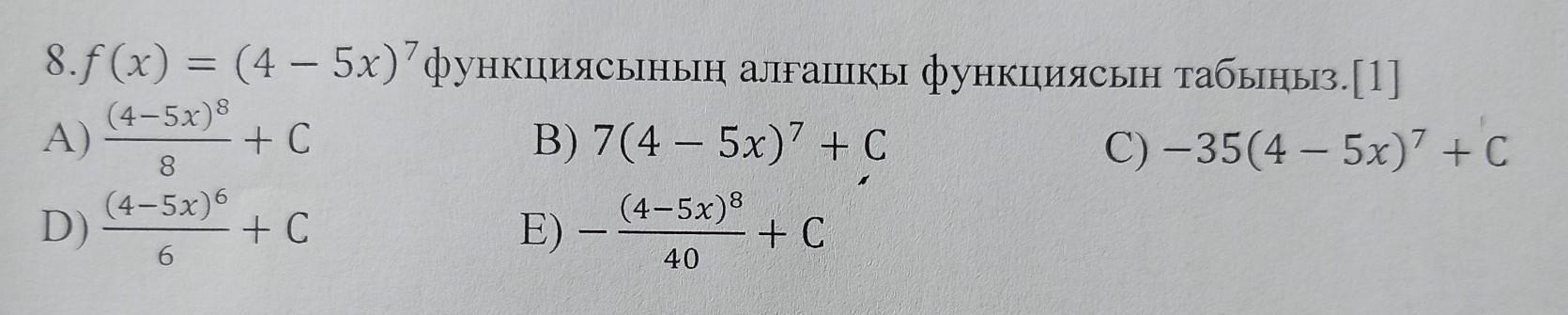Ответы
Ответ дал:
1
Ответ: Е) -(4-5x)⁸/40+c;
Объяснение:
первообразной для функции f(x)=(4-5x)⁷ является функция
F(x)=((4-5x)⁸/(8*(-5)))+c; F(x)=-(4-5x)⁸/40+c;
- это формлуа Е)
Действительно, F'(x)=(-(4-5x)⁸/40+c)'=-(8*(-5)(4-5x)⁷/40)+0=(4-5x)⁷ =f(x)
Ответ дал:
1
Ответ:
Первообразной для функции f(x) является функция F(x) , если
.
Действительно, .
Применили правило дифференцирования сложной функции .
Если учили интегралы, то
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад