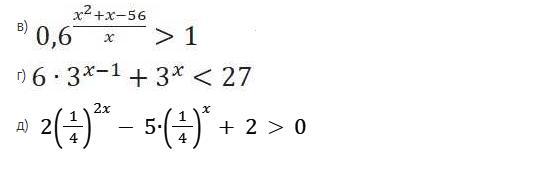Ответы
Ответ дал:
1
Ответ:
Объяснение: (^ -знак степени)
в) вместо 1 пишем 0,6^0, т.к. основание <1, то (x^2 +x-56)/x <0,
(x-7)(x+8)/x <0, метод интервалов,
_____-___(-8)___+____(0)____-___(7)____+____, надо < 0,
отв. (-Б; -8) u (0;7)
г) 6*3^x *1/3 +3^x <27, 2*3^x +3^x <27, 3*3^x <27, 3^x <3^2,
основание 3> 1, x<2, отв. (-Б; 2)
д) пусть (1/4)^x =t, 2t^2-5t+2>0, D=9, t1= 1/2, t2=2, метод интервалов
____+___(1/2)_____-____(2)____+___ t, надо >0, t<1/2 или t>2,
обратная замена: (1/4)^x <1/2, (1/2)^2x <1/2, 2x>1, x>1/2,
(1/4)^x>2, (1/2)^2x >(1/2)^-1, 2x <-1, x<-1/2, отв. (-Б;-1/2)u(1/2; +Беск.)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад