В прямоугольном треугольнике ABC на катете AC отмечена точка D такая, что ∠ABD=2∠DBC. Точка E лежит на гипотенузе BC, F — основание перпендикуляра из E на прямую BD. Оказалось, что BF=BA. Докажите, что DE+EF=AD. (Ответите верно, получите метку "лучший" ответ)
Ответы
Ответ дал:
2
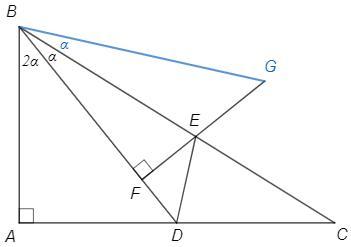
Возьмем на продолжении FE точку G такую, что ∠GBC=∠DBC
△ABD=△FBG по катету (BA=BF) и острому углу (∠ABD=2∠DBC=∠FBG)
=> BD=BG, AD=FG
△DBE=△GBE по двум сторонам и углу между ними => DE=EG
AD =FG =FE+EG =EF+DE
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад