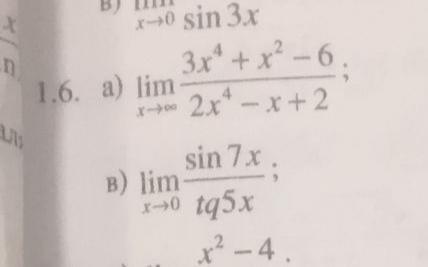Question

ОЧЕНЬ СРОЧНО ПОМОГИТЕ РЕШИТЬ ЗАДАНИЕ ПО МАТЕМАТИКЕ
ДАМ 100 БАЛЛОВ
задание 1.6 А

Answer 1

Ответ:

а) $\displaystyle \lim_{x \to \infty} \frac{3+\frac{1}{x^2} -\frac{6}{x^4} }{2 -\frac{1}{x^3} +\frac{2}{x^4} }=1,5$

б) $\displaystyle \lim_{x \to 0} \frac{sin7x}{tg5x}=1,4$

Пошаговое объяснение:

Требуется найти предел последовательности.

а) $\displaystyle \lim_{x \to \infty} \frac{3x^4+x^2-6}{2x^4-x+2}$

При $x \rightarrow \infty$ приходим к неопределенности типа $\displaystyle [\frac{\infty}{\infty} ]$. В таком случае, нужно все члены в числителе и знаменателе разделить на х в наивысшей степени:

$\displaystyle \lim_{x \to \infty} \frac{3x^4+x^2-6}{2x^4-x+2}=\displaystyle \lim_{x \to \infty} \frac{\frac{3x^4}{x^4} +\frac{x^2}{x^4} -\frac{6}{x^4} }{\frac{2x^4}{x^4} -\frac{x}{x^4} +\frac{2}{x^4} }= \lim_{x \to \infty} \frac{3+\frac{1}{x^2} -\frac{6}{x^4} }{2 -\frac{1}{x^3} +\frac{2}{x^4} }$

Все дроби в знаменателе, которых есть х в какой либо степени, будут стремится к нулю при , и называются бесконечно малыми.

$\displaystyle \lim_{x \to \infty} \frac{3+\frac{1}{x^2} -\frac{6}{x^4} }{2 -\frac{1}{x^3} +\frac{2}{x^4} }=\frac{3+0-0}{2-0+0} =\frac{3}{2} =1,5$

Предел суммы, разности, частного равен сумме, разности, частному пределов.

$\displaystyle \lim_{x \to \infty} \frac{3+\frac{1}{x^2} -\frac{6}{x^4} }{2 -\frac{1}{x^3} +\frac{2}{x^4} }=\frac{\lim_{x \to \infty}3+\lim_{x \to \infty}\frac{1}{x^2}-\lim_{x \to \infty} \frac{6}{x^4} }{\lim_{x \to \infty}2-\lim_{x \to \infty}\frac{1}{x^3}+\lim_{x \to \infty}\frac{2}{x^4} }$

Все дроби в знаменателе, которых есть х в какой либо степени, будут стремится к нулю при $x \rightarrow \infty$, и называются бесконечно малыми.

$\displaystyle \frac{\lim_{x \to \infty}3+\lim_{x \to \infty}\frac{1}{x^2}-\lim_{x \to \infty} \frac{6}{x^4} }{\lim_{x \to \infty}2-\lim_{x \to \infty}\frac{1}{x^3}+\lim_{x \to \infty}\frac{2}{x^4} }=\frac{3+0-0}{2-0+0} =\frac{3}{2} =1,5$

б) $\displaystyle \lim_{x \to 0} \frac{sin7x}{tg5x}$

При $x \rightarrow 0$ приходим к неопределенности типа $\displaystyle [\frac{0}{0} ]$.

Воспользуемся первым замечательным пределом и ее следствием: $\displaystyle \lim_{x \to 0} \frac{sinx}{x}=1, \ \ \displaystyle \lim_{x \to 0} \frac{tgx}{x}=1$.

Числитель и знаменатель умножим на переменную, а далее штучно введем множители, которые фигурируют как аргументы синуса и тангенса.

$\displaystyle \lim_{x \to 0} \frac{sin7x*5x*\frac{1}{5} }{tg5x*7x*\frac{1}{7} }$

Предел произведения/частного равен произведению частному пределов.

$\displaystyle \lim_{x \to 0} \frac{sin7x*5x*\frac{1}{5} }{tg5x*7x*\frac{1}{7} }= \lim_{x \to \ 0} \frac{sin7x}{7x} * \lim_{x \to \ 0} \frac{5x}{tg5x} * \lim_{x \to 0}\frac{1}{5}: \lim_{x \to 0}\frac{1}{7}$

Таким образом получили два замечательных предела и числовые множители:

$\displaystyle \lim_{x \to \ 0} \frac{sin7x}{7x} * \lim_{x \to \ 0} \frac{5x}{tg5x} * \lim_{x \to 0}\frac{1}{5}: \lim_{x \to 0}\frac{1}{7}= 1*1*{\frac{1}{5} :\frac{1}{7} =\frac{7}{5} =1,4$