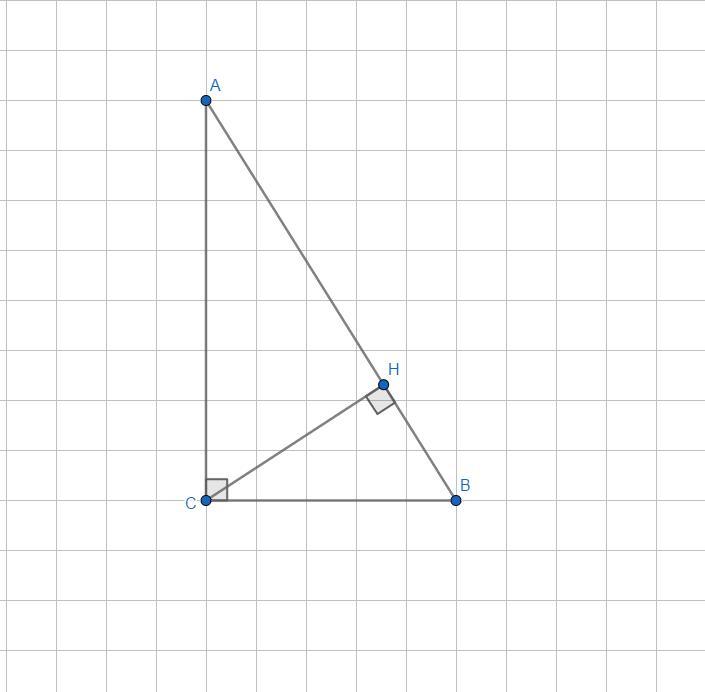
В треугольнике ABC угол C равен 90 , ° CH — высота, AB = 90, sin A=1:3
Найдите длину
отрезка BH. 10 баллов
Ответы
Ответ дал:
1
Ответ:
- BH=10 ед.
Объяснение:
Дано:
ΔABC
∠C=90°
CH⊥AB
AB=90 ед.
Найти: BH - ?
Решение:
- Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
, откуда
ед.
- Синусы равных углов равны.
Т.к. ∠B - общий у прямоугольных треугольников ΔABC и ΔCBH, то ∠A=∠BCH, значит .
Тогда , откуда
ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад