Question

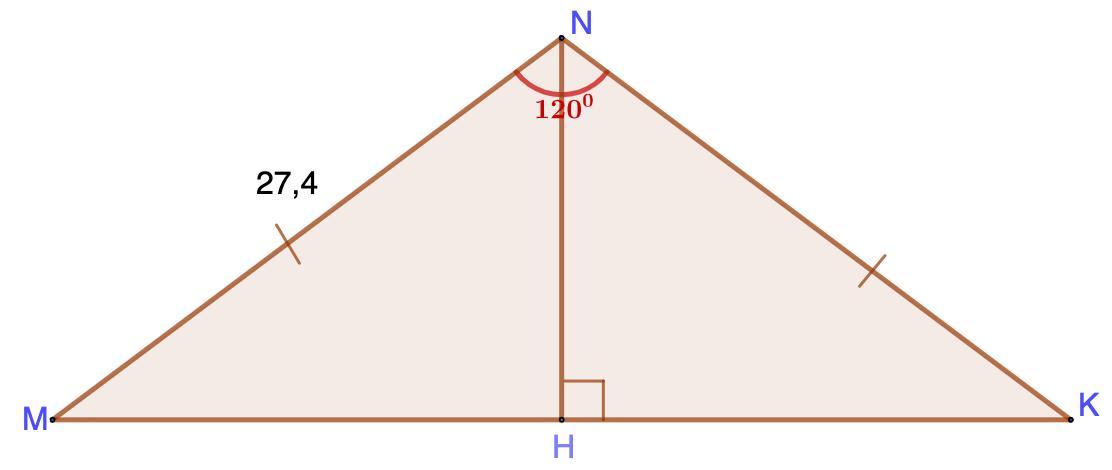
Реши задачу. В равнобедренном треугольнике MNK боковые стороны равны 27, 4 см, а угол, противолежащий основанию, равен 120 °. Определи расстояние от вершины этого угла до основания треугольника MNK.​

Answer 1

Ответ:

Расстояние от вершины угла, противолежащего основанию,  до основания треугольника MNK равно 13,7 см.

Объяснение:

Требуется определить расстояние от вершины этого угла до основания треугольника MNK.​

Дано: ΔMNK - равнобедренный;

МN = 27,4 см;

∠N = 120°.

Найти: расстояние от вершины угла, противолежащего основанию,  до основания треугольника MNK.​

Решение:

1. Рассмотрим ΔMNK - равнобедренный.

• Расстояние от точки до прямой есть длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ NН - высота.

• Сумма углов треугольника равна 180°.

⇒ ∠М + ∠N + ∠K = 180°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠М =∠K =( 180° - 120°) : 2 = 30°

2. Рассмотрим ΔMNH - прямоугольный.

∠М = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ NH = MN : 2 = 27,4 : 2 = 13,7 (см)

Расстояние от вершины угла, противолежащего основанию,  до основания треугольника MNK равно 13,7 см.