Question

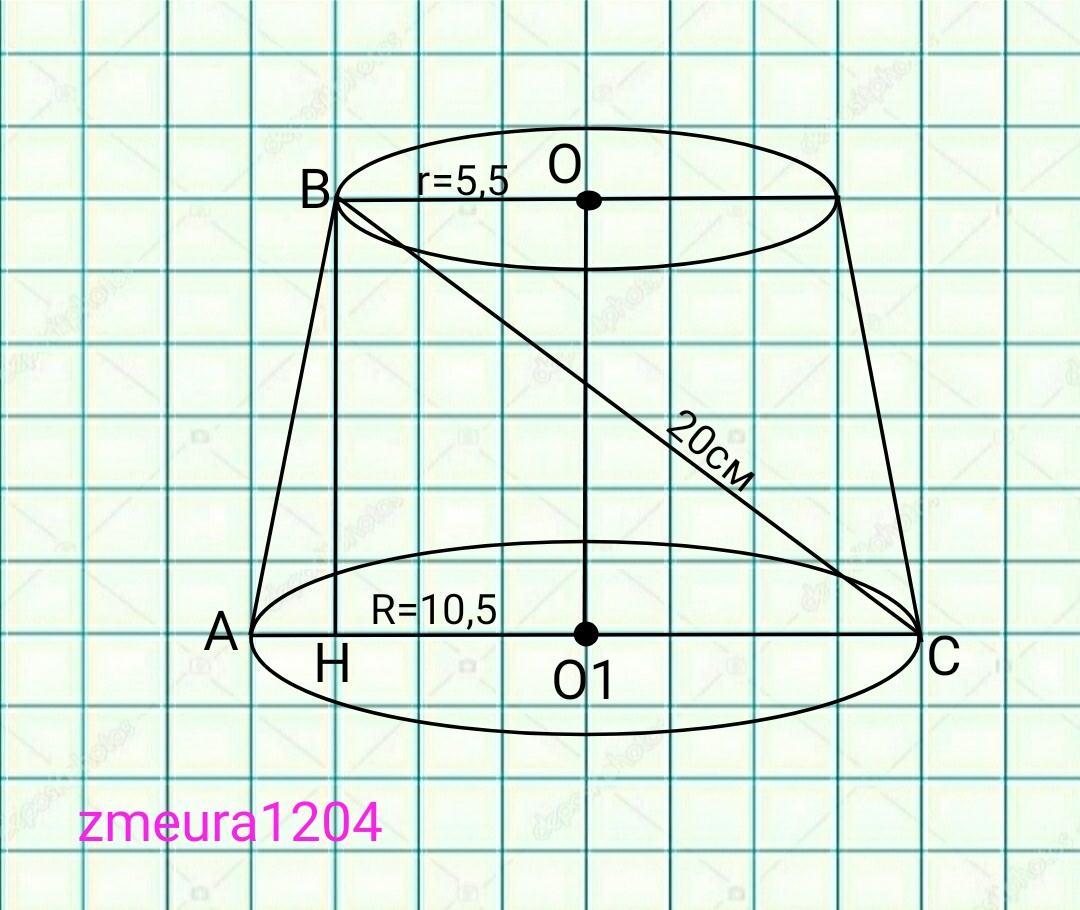
Диагональ осевого сечения усечённого конуса = 20 см. , а радиусы его оснований 10,5 см. и 5,5 см. Найдите площадь боковой поверхности этого усечённого конуса .​

Answer 1

Ответ:
Sбок=208π см²

Решение:
АН=R-r=10,5-5,5=5см
АС=2R=2*10,5=21см.
НС=АС-АН=21-5=16см
∆ВНС- прямоугольный треугольник
По теореме Пифагора
ВН=√(ВС²-НС²)=√(20²-16²)=
=√(400-256)=√144=12см.
∆АВН- прямоугольный треугольник
По теореме Пифагора
АВ=√(ВН²+АН²)=√(12²+5²)=
=√(144+25)=√169=13см
Sбок=π(r+R)*AB=π(5,5+10,5)*13=
=13π*16=208π см²