ПОМОГИТЕ ПОЖАЛУЙСТА ОООЧЕНЬ НАДО !!! НАПИШИТЕ УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГНАФИКУ ФУНКЦИИ y=f(x) в точке х0. Задание 7 и 8.
Приложения:
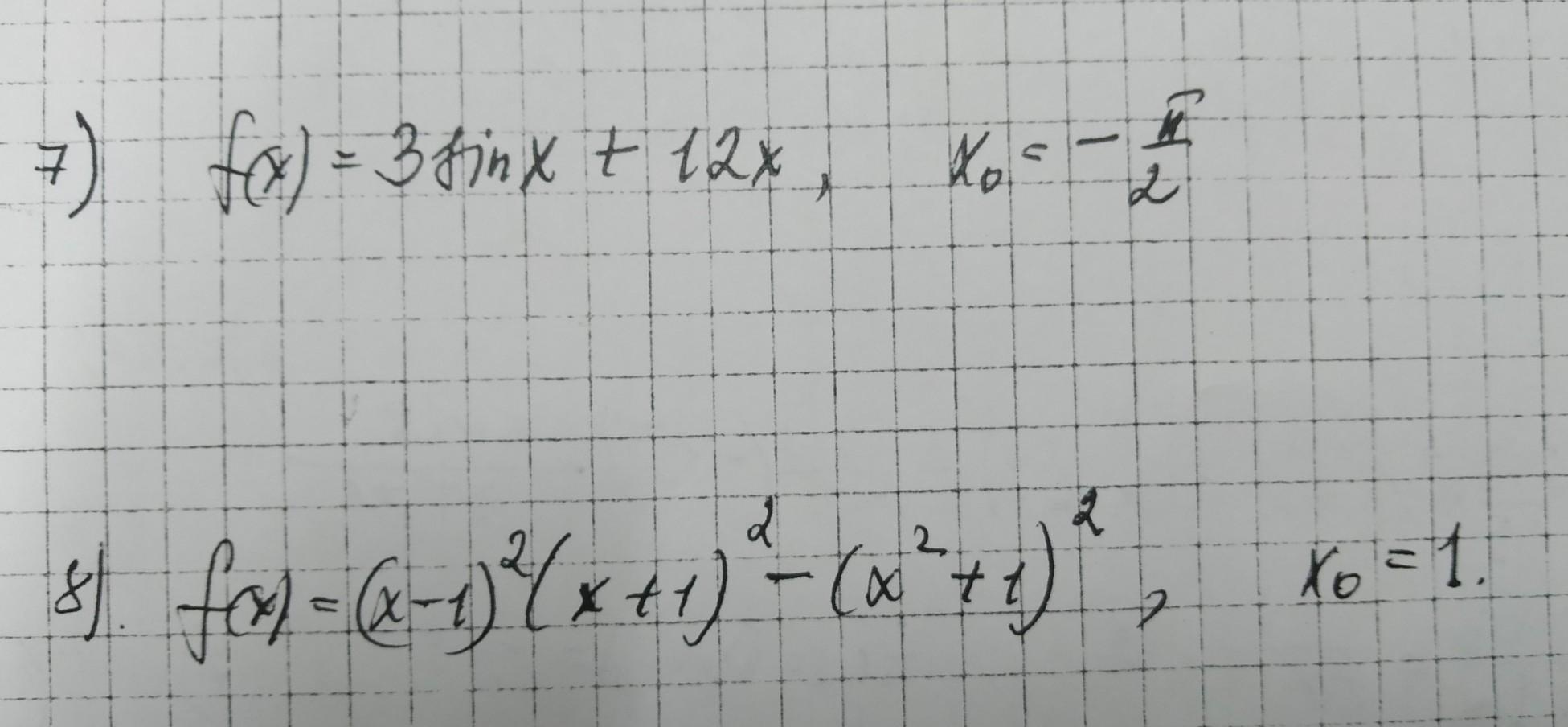
Ответы
Ответ дал:
1
Объяснение:
7)
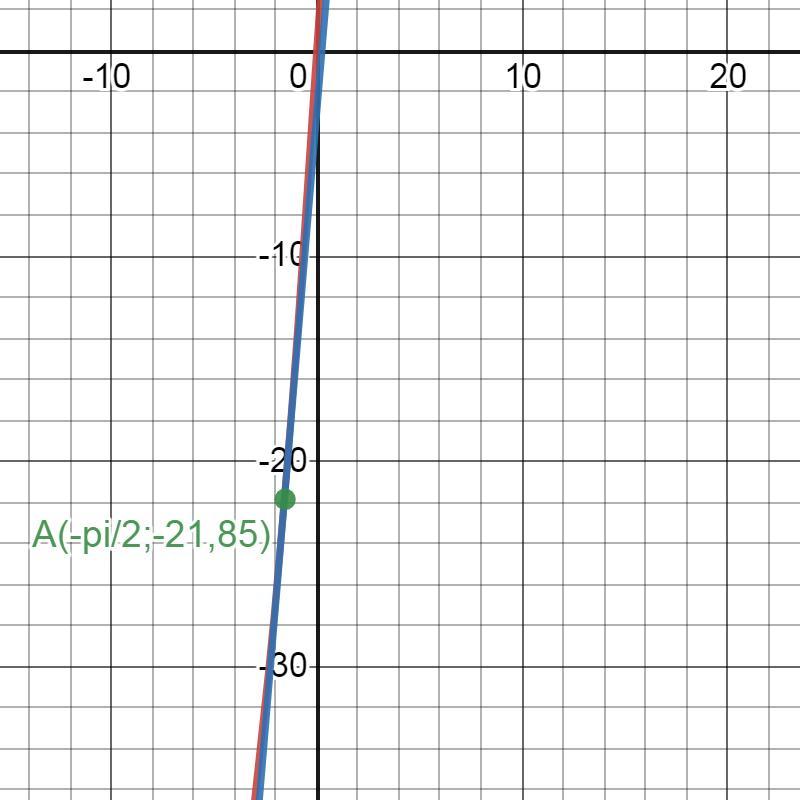
Ответ: yk=12x-3.
8)
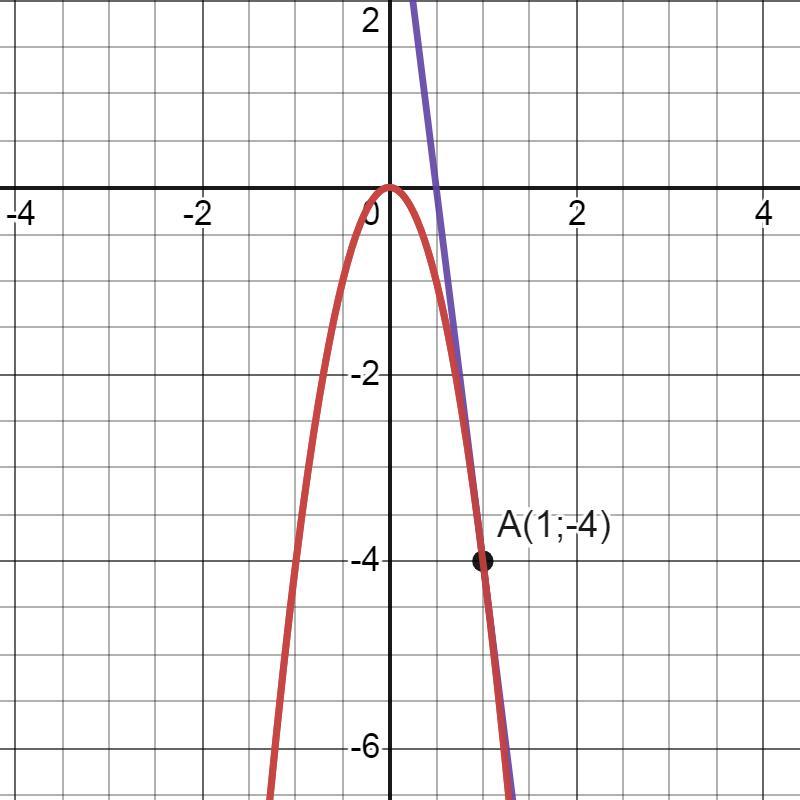
Ответ: yk=-8x+4.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад