Question

высота конуса равна 8 см высота вписанного в него цилиндра равна 6 см. образующая конуса равна 10 см найти S боковой поверхности цилиндра

Answer 1

Ответ:

56.55 см²

Пошаговое объяснение:

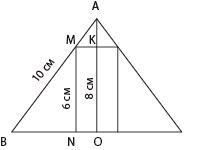
Рассмотрим разрез фигур по осевой линии (см приложение)

В прямоугольном треугольнике AOB АВ - образующая конуса = 10 см, а высота AO = 8 см, тогда радиус конуса равен:

BO = √(AB²-BO²) = √(10²-8²) = √36 = 6 см

Треугольник AKM подобен треугольнику AOB, следовательно

AK/AO = MK/BO

Вычислим отсюда MK:

MK = (AK/AO) * BO = 2/8 * 6 = 6/4 = 1.5 см

Площадь боковой поверхности цилиндра рассчитывается по формуле:

S = 2πRh

где R - радиус цилиндра = MK

S = 2π*MK*h = 2π*1.5*6 = 56.55 см²