Question

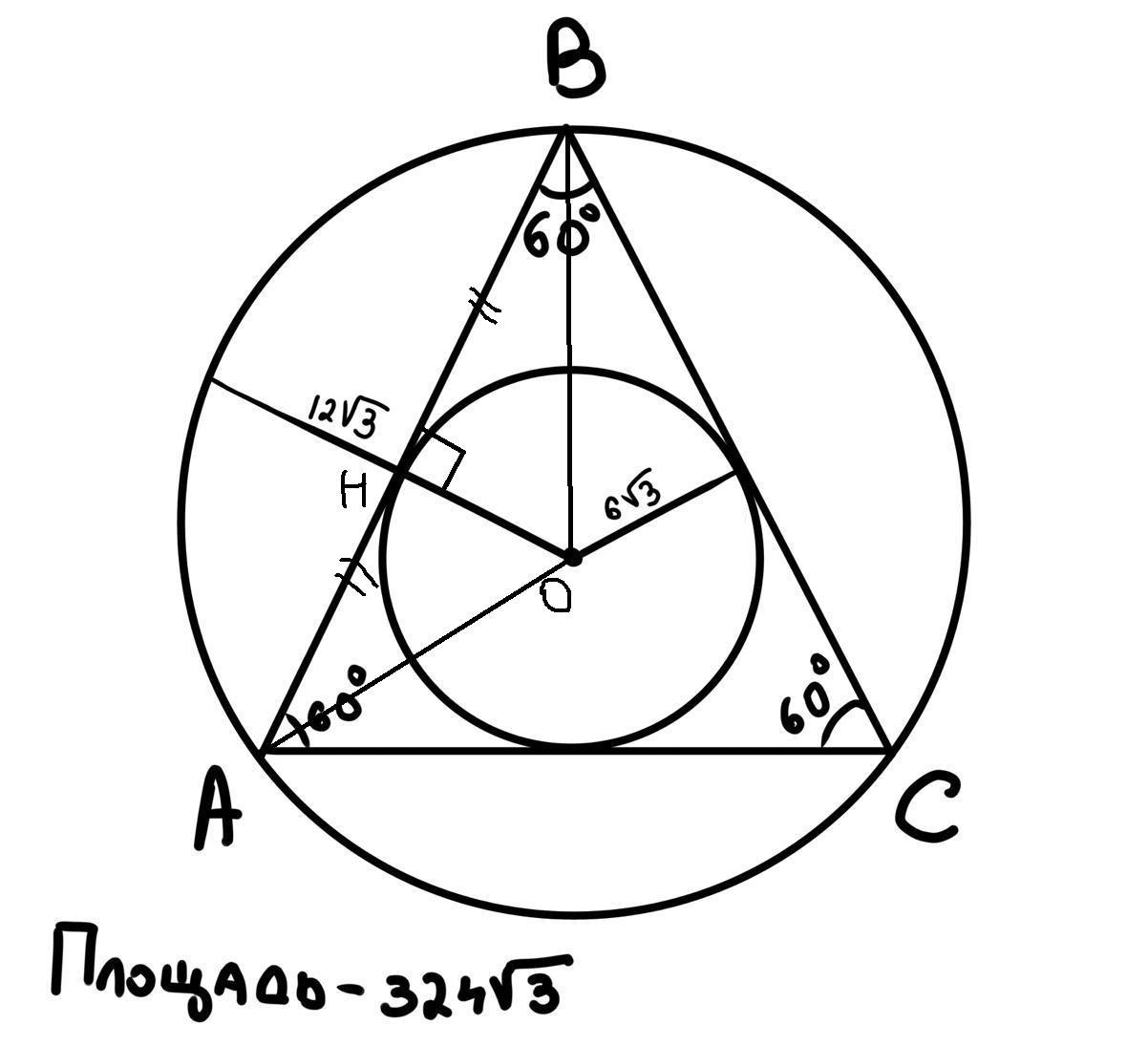
Нужно найти длину меньшей дуги АВ.
Срочно, пожалуйста!

Answer 1

Ответ:

$L = 8\pi \sqrt{3}$

Объяснение:

1) Длина дуги AB вычисляется по формуле $L = \alpha R$, где R - радиус окружности, $\alpha$ - центральный угол дуги в радианах.

Так как ΔАВС - правильный (все углы равны), центр вписанной окружности совпадает с центром описанной окружности, значит $\alpha$ = ∠AOB, где O - центр вписанной (маленькой) окружности.

2) AB - касательная к вписанной окружности, значит OH ⊥ AB (см. рис.). Кроме того, центр вписанной окружности лежит на серединной перпендикуляре к стороне треугольника, значит AH = BH. Таким образом, в ΔAOB медиана совпадает с высотой, значит он равнобедренный с основанием AB, ∠ABO = ∠BAO

3) В правильном треугольнике центр вписанной окружности лежит на биссектрисах его углов, значит ∠ABO = 0.5 * ∠ABC = 30°.

По теореме о сумме углов треугольника ∠AOB = 180° - (∠ABO + ∠BAO) = 180° - (30° + 30°) = 120°

4) $L = \alpha R$ (п. 1). Подставим значения $\alpha$ = ∠AOB (п. 1) и R = 12√3 (условие)

∠AOB = 120° (п. 3) = 2π/3 (радиан)

$L = \frac{2\pi }{3} * 12\sqrt{3} = 2\pi *4\sqrt{3} = 8\pi \sqrt{3}$