Срочно!! даю 30 баллов! с решением! Найдите отношение стороны правильного треугольника, вписанного в окружность, к стороне правильного треугольника, описанного около этой окружности.
Ответы
Ответ дал:
2
Ответ:
Отношение сторон равно k = 1/2.
Объяснение:
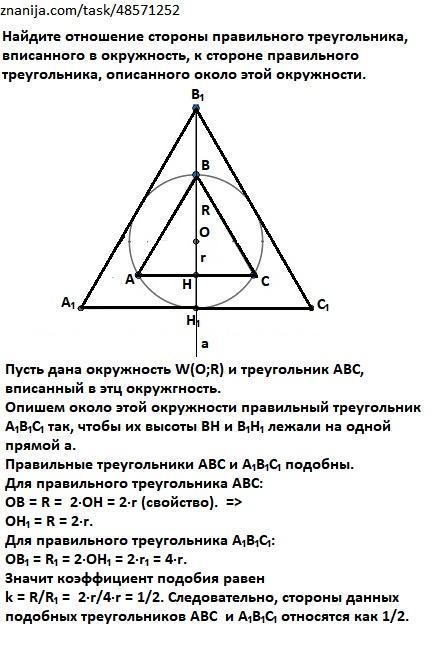
Пусть дана окружность W(O;R) и треугольник АВС, вписанный в эту окружность.
Опишем около этой окружности правильный треугольник А₁В₁С₁ так, чтобы их высоты ВН и В₁Н₁ лежали на одной прямой а.
Правильные треугольники АВС и А₁В₁С₁ подобны.
Для правильного треугольника АВС:
ОВ = R = 2·ОН = 2·r (свойство). =>
Отрезок ОН₁ = R = 2·r.
Для правильного треугольника А₁В₁С₁:
OB₁ = R₁ = 2·ОН₁ = 2·r₁ = 4·r.
Значит коэффициент подобия равен
k = R/R₁ = 2·r/4·r = 1/2. Следовательно, стороны данных подобных треугольников АВС и А₁В₁С₁ относятся как 1/2.
Приложения:
Аноним:
Вы удалили мой ответ, написав что я скопировала его с предыдущего ответа….)
но там даже следа от копии нет)
там просто ошибка ) я вместо х-40 написала 2х) пожалуйста, перед тем как обвинять кого-то проверяйте, какой бред вы написали)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад