Question

шестикутник усі сторони якого рівні і дорівнюють 12 см вписаний у коло радіуса 10 см. знайдіть відстані від центра кола до сторін шестикутника​

Answer 1

Ответ:

Расстояние от центра окружности до стороны шестиугольника  равно 8 см.

Объяснение:

Пусть дан шестиугольник , вписанный в окружность радиуса 10 см. Стороны шестиугольника равны 12 см.

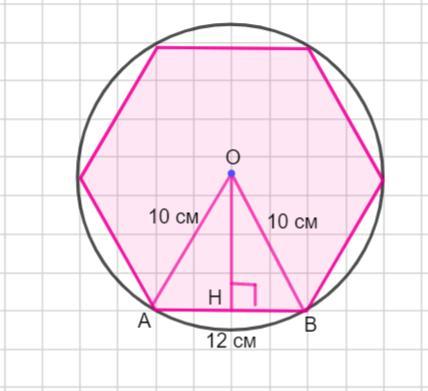
На рисунке АВ =12 см, АО=ВО = 10 см.

Δ АОВ - равнобедренный. Высота ОН, проведенная к основанию является медианой. Тогда АН =ВН= 12: 2 =6 см.

Рассмотрим Δ ОНВ - прямоугольный.

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$OB^{2} =OH^{2} +BH^{2} ;\\OH^{2}=OB^{2}-BH^{2};\\OH=\sqrt{OB^{2}-BH^{2}} ;\\OH=\sqrt{10^{2} -6^{2} } =\sqrt{100-36} =\sqrt{64} =8$

Значит, расстояние от центра окружности до стороны шестиугольника  равно 8 см.