Question

Найдите высоту правильной четырёхугольной усечённой пирамиды со сторонами в основаниях 6 и 12, если боковые грани наклонены к плоскости основания под углом 60°.

Answer 1

Ответ:

$3\sqrt{3}$

Объяснение:

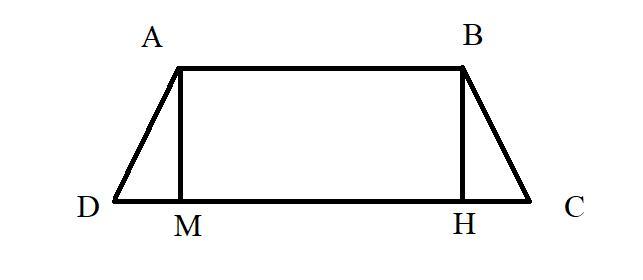
Если рассмотреть сечение пирамиды в плоскости, перпендикулярной основанию и двум сторонам основания (если смотреть сверху), то получится трапеция со основаниями AB=6 и CD=12 (см рисунок).
Угол BCD=60 градусов по условию.  DM+HC=DC-AB=6, также DM=HC, то есть HC=3. BH=tg(60)*HC=$\sqrt{3}*HC=3\sqrt{3}$
P.S. Рисунок схемотичный, пиксели не высчитывал)