Question

Даю 100 баллов. CD || AB
Довести AB = AD

Answer 1

Объяснение:

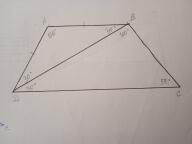
Дано:   АВСD - трапеция, CD || AB, ВD - диагональ, ∠СВD=100°, ∠BCD=50°. Докажем, что АВ=AD.

ΔВСD;  ∠BDC=180-100-50=30°

∠ABD=∠BDC=30° как внутренние накрест лежащие при CD || AB и секущей BD.

ΔADB;  ∠ADB=180-120-30=30°

ΔADB - равнобедренный, т.к. углы при основании равны.

Значит AB = AD. Доказано.

Answer 2

Ответ:

ΔВСD; ∠BDC=180-100-50=30°

∠ABD=∠BDC=30° как внутренние накрест лежащие при CD || AB и секущей BD.

ΔADB; ∠ADB=180-120-30=30°

ΔADB - равнобедренный, т.к. углы при основании равны.

Объяснение: