Question

Сокол-пустельга, летящий на высоте 40 м, видит в траве отдельных мышей. Оцените угол между лучами, различимыми соколом как отдельные, если размер тела полевой мыши принять равной 12 см. В силу малости угла принять, что тангенс угла равен углу в радианах. Ответ в радианах округлите до сотых и запишите без указания единиц измерения и дополнительных символов.

Answer 1

Ответ:

Угол между лучами, различимыми соколом как отдельные, равен 0,003 рад.

В ответ нужно записать 0,003.

Объяснение:

Сокол-пустельга, летящий на высоте 40 м, видит в траве отдельных мышей. Оценить угол между лучами, различимыми соколом как отдельные, если размер тела полевой мыши принять равной 12 см.

1) Пусть сокол видит мышь под некоторым углом α.
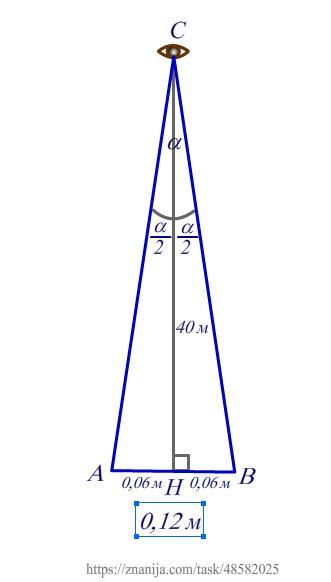
В треугольнике ABC стороны AC и BC - это лучи, которые образуют угол α, сторона AB - длина тела мыши.

1 м = 100 см.

AB = 12 см = 0,12 м.

2) ΔABC равнобедренный, высота СН - это расстояние от сокола до полевой мыши.

CH = 40 м.

Высота в равнобедренном треугольнике является его медианой и биссектрисой.

Тогда ∠HCB = α/2.

HB = AB : 2 = 0,12 м : 2 = 0,06 м.

• В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему.

3) Так как угол α очень мал, то tg α/2 ≈ α/2.

$\displaystyle tg \frac{\alpha}{2} \approx \frac{\alpha}{2} = \frac{0,06}{40}=0,0015.$

α = 0,0015 · 2 = 0,003 (рад).

Угол между лучами, различимыми соколом как отдельные, равен 0,003 рад.