Question

Діагональ прямокутника довжиною 10 см утворює кут з його стороною, синус якого дорівнює 0,6. Знайдіть площу прямокутника.
Відповідь надати у квадратних сантиметрах.

Answer 1

Ответ:

Площадь прямоугольника равна 48 см².

Объяснение:

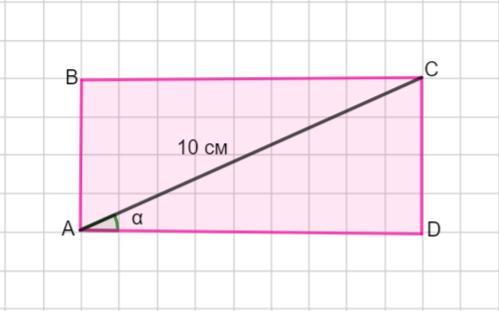
Пусть дан прямоугольник АВСD.  Диагональ АС =10 см .

∠АСD=α. По условию  sinα=0,6.

Рассмотрим Δ АСD - прямоугольный.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе .

Значит,

$sin\alpha =\dfrac{CD }{AC} ;\\\\\dfrac{6}{10} =\dfrac{CD}{10} ;\\\\CD=6$

Одна сторона прямоугольника равна 6 см.

Найдем другой катет по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AC^{2} =AD^{2} +CD^{2} ;\\AD^{2} =AC^{2} -CD^{2} ;\\AD= \sqrt{AC^{2} -CD^{2} } ;\\AD =\sqrt{10^{2} -6^{2} } =\sqrt{100-36} =\sqrt{64} =8$

Тогда другая сторона прямоугольника 8 см.

Чтобы найти площадь прямоугольника, надо одну сторону умножить на другую

$S= 6\cdot8=48$  cм².

Площадь прямоугольника равна 48 см².