СРОЧНО!!! M, N, P, Q, R, S являются центрами сторон произвольного шестиугольника. Нужно доказать, что векторы MN+PQ+RS =0 (тоже вектор)
Приложения:
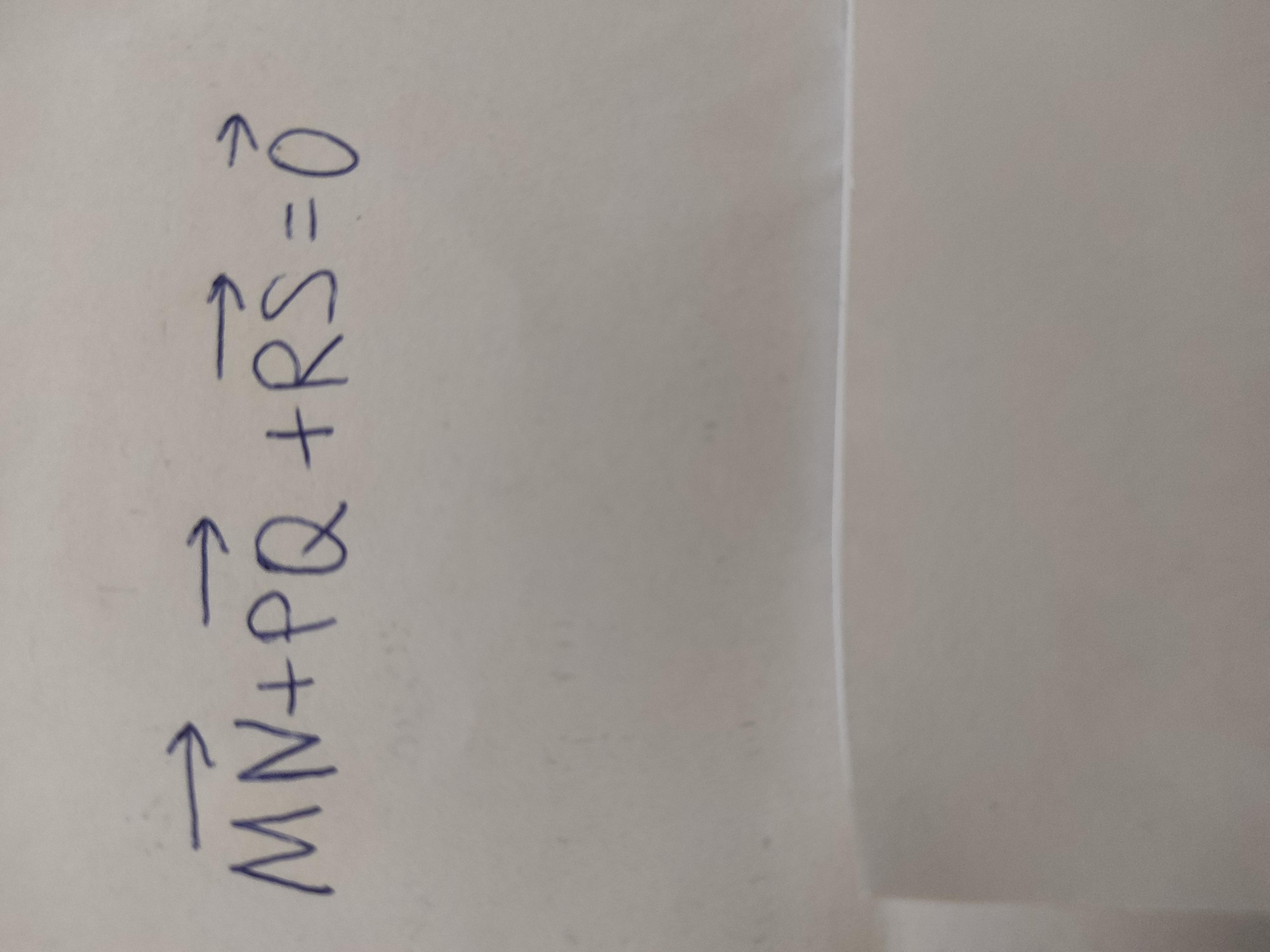
orjabinina:
а название шестиугольника?
не написаноб скорее всего ABCDEF
Ответы
Ответ дал:
1
M, N, P, Q, R, S являются центрами сторон произвольного шестиугольника. Нужно доказать, что сумма векторов MN+PQ+RS =0
Объяснение:
Пусть шестиугольник А₁А₂А₃А₄А₅А₆
1)Для ΔА₁А₂А₃ отрезок MN- средняя линия . По свойству средней линии треугольника MN=1/2* А₁А₃ . Тогда векор .
2)Для ΔА₃А₄А₅ отрезок PQ- средняя линия . По свойству средней линии треугольника PQ=1/2* А₃А₅ . Тогда векор .
3)Для ΔА₁А₅А₆ отрезок RS- средняя линия . По свойству средней линии треугольника RS=1/2* А₁А₅ . Тогда векор .
4)Тогда , учтем , что вектора
противоположно направленные .
.
Приложения:

Спасибо большое, теперь все понятно, если не трудно, решите еще одну задачку по геометрии, она в моем профиле
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад