Ответы
Ответ дал:
0
Ответ:
Объяснение:
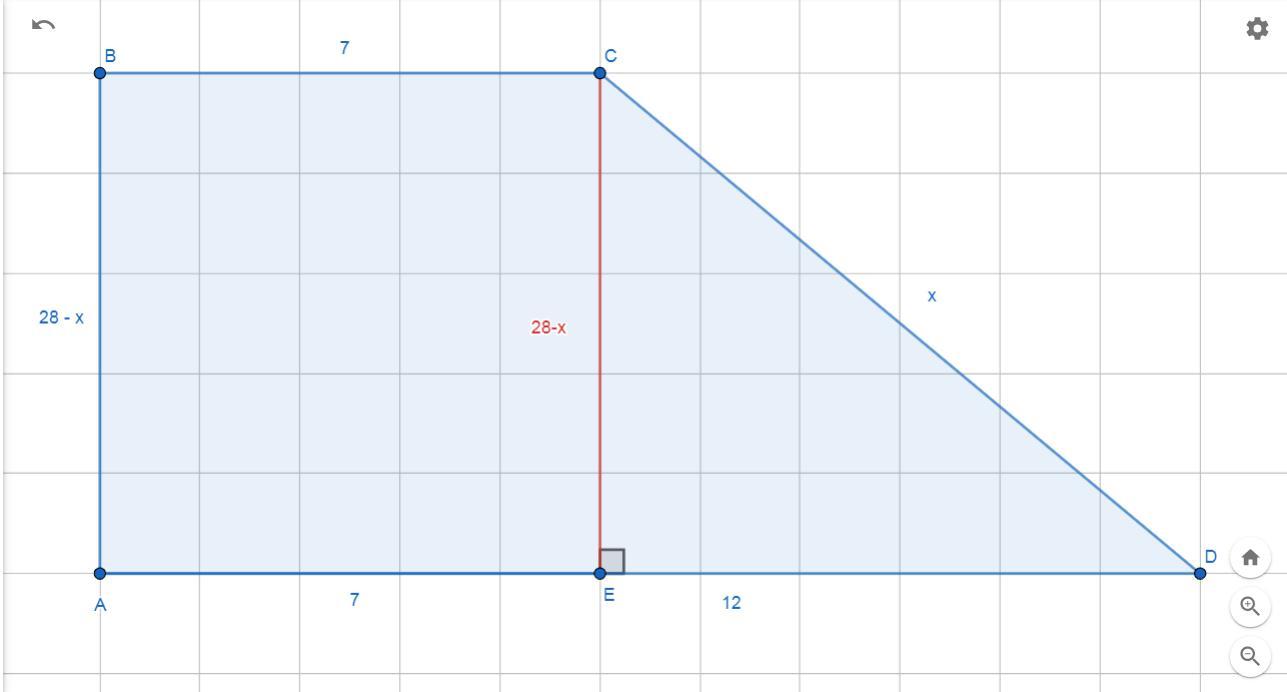
Пусть CD = x
Раз сумма оснований равна BC+AD = 7+19 = 26
То сумма двух других сторон
AB+BC+CD+AD = 44
AB+CD = 44-16
AB+CD = 28
AB = 28 -CD = 28-x
Найдем длину ED
ED = AD-BC = 19-7 =12
По теореме Пифагора
CE² +ED² = CD²
(28-x)² + 12² = x²
784-56x+x² +144 = x²
56x=144+784
56x =928
Вычислим площадь трапеции
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад