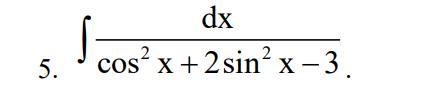Question

Помогите с интегралом

Answer 1

Ответ:

$\boxed{ \boxed{\rm \int {\frac{dx}{\cos^{2} x + 2 \sin^{2} x - 3} } \, = \frac{\sqrt{2} \ arctg \ (\sqrt{2} \ ctg \ x ) }{2} + C = - \frac{ \ arctg \ \bigg (\dfrac{tg \ x}{\sqrt{2} } \bigg ) }{\sqrt{2} } + C} }$

Примечание:

По таблице первообразных:

$\boxed{\rm \displaystyle \int {\frac{dx}{a^{2} + x^{2} } } \, dx = \frac{1}{a} arctg \ \frac{x}{a} + C}$

$\boxed{\rm \sin^{2} x = \dfrac{1}{\rm 1 + ctg^{2}x} }$

$\boxed{ -\dfrac{1}{\sin^{2} x} = - (\rm 1 + ctg^{2}x) }$

Пошаговое объяснение:

• 1) способ решения

$\boxed{\rm \int {\frac{dx}{\cos^{2} x + 2 \sin^{2} x - 3} } \, = \frac{\sqrt{2} \ arctg \ (\sqrt{2} \ ctg \ x ) }{2} + C}$

а) преобразуем знаменатель подынтегрального выражения:

$\rm \cos^{2} x + 2 \sin^{2} x - 3 =\cos^{2} x + \sin^{2} x + \sin^{2} x - 3 = 1 + \sin^{2} x - 3 =$

$\rm = -3 + 1 + \sin^{2} x = -2 + \sin^{2} x = \sin^{2} x - 2 = \dfrac{1}{\rm 1 + ctg^{2}x} -2 =$

$\rm = \dfrac{1}{\rm 1 + ctg^{2}x} - \dfrac{\rm 2(1 + ctg^{2}x)}{\rm 1 + ctg^{2}x} = \dfrac{\rm 1 - 2(1 + ctg^{2}x)}{\rm 1 + ctg^{2}x} = \dfrac{\rm 1 - (2 + 2ctg^{2}x)}{\rm 1 + ctg^{2}x} =$

$\rm = \dfrac{\rm 1 - 2 - 2ctg^{2}x}{\rm 1 + ctg^{2}x} = \dfrac{\rm -1 - 2ctg^{2}x}{\rm 1 + ctg^{2}x} = - \dfrac{\rm 1 + 2ctg^{2}x}{\rm 1 + ctg^{2}x}$

(При взятии интеграл выполнена замена переменной; описании замены находится после взятия интеграла!)

$\rm \displaystyle \int {\frac{dx}{\cos^{2} x + 2 \sin^{2} x - 3 } = \int {\frac{dx}{ - \dfrac{\rm 1 + 2ctg^{2}x}{\rm 1 + ctg^{2}x} } = -\int {\frac{\dfrac{dx}{1} }{ \dfrac{\rm 1 + 2ctg^{2}x}{\rm 1 + ctg^{2}x} } =$

$\rm \displaystyle = - \int {\frac{ \rm 1 + ctg^{2}x }{ \rm 1 + 2ctg^{2}x }\, dx = - \int {\frac{ \rm (1 + ctg^{2}x) }{ \rm 1 + 2ctg^{2}x } \cdot (-1) \cdot \dfrac{dt}{(1 + ctg^{2} x)} }\, =$

$\rm \displaystyle = \int {\frac{ \rm dt }{ \rm 1 + 2ctg^{2}x } = \int {\frac{ \rm dt }{ \rm 1 + 2t^{2} } = \frac{1}{2} \int {\frac{ \rm dt }{ \rm \bigg(\dfrac{1}{2} + t^{2} \bigg) } = \frac{1}{2} \int {\frac{ \rm dt }{ \rm \bigg( \bigg(\sqrt{\dfrac{1}{2}} \bigg)^{2} + t^{2} \bigg) } =$

$\rm \displaystyle = \frac{1}{2} \int {\frac{ \rm dt }{ \rm \bigg( \bigg(\dfrac{1}{\sqrt{2} }\bigg)^{2} + t^{2} \bigg) } = \frac{1}{2} \cdot \frac{\dfrac{1}{1} }{\dfrac{1}{\sqrt{2} } } \ arctg \ \bigg(\frac{\dfrac{t}{1} }{\dfrac{1}{\sqrt{2} } } \bigg) + C = \frac{\sqrt{2} \ arctg \ (t\sqrt{2} ) }{2} + C =$

$\rm \displaystyle = \frac{\sqrt{2} \ arctg \ (\sqrt{2} \ ctg \ x ) }{2} + C;$

---------

$\rm \dfrac{d}{dx} (ctg \ x) = -\dfrac{1}{\sin^{2} x} = - (\rm 1 + ctg^{2}x)$

Замена: $\rm t = ctg \ x \Longrightarrow \boxed{\rm t^{2} = ctg^{2} x}$

$\rm dt = d(ctg \ x) \ dx \Longrightarrow \boxed{\rm dx = \dfrac{dt}{d(ctg \ x)} = - \dfrac{dt}{1 + ctg^{2} x} }$

• 2) способ решения

$\boxed{\rm \int {\frac{dx}{\cos^{2} x + 2 \sin^{2} x - 3} } \, = - \frac{ \ arctg \ \bigg (\dfrac{tg \ x}{\sqrt{2} } \bigg ) }{\sqrt{2} } + C}$

а) преобразуем знаменатель подынтегрального выражения:

$\rm \cos^{2} x + 2 \sin^{2} x - 3 =\cos^{2} x + \sin^{2} x + \sin^{2} x - 3 = 1 + \sin^{2} x - 3 =$

$\displaystyle \rm = -3 + 1 + \sin^{2} x = -2 + \sin^{2} x = \sin^{2} x - 2 = \frac{\rm 1 - \cos 2x}{\rm 2} - 2 = \frac{\rm 1 - \cos 2x - 4}{\rm 2} =$

$\displaystyle \rm = \frac{\rm 1 - \cos 2x - 4}{\rm 2} = \frac{\rm -3 - \cos 2x}{\rm 2} = -\frac{\rm 3 + \cos 2x}{\rm 2}$

$\displaystyle \rm \int {\frac{dx}{\cos^{2} x + 2 \sin^{2} x - 3} } \, = \int {\frac{\dfrac{dx}{1} }{ -\dfrac{\rm 3 + \cos 2x}{\rm 2} } \, = -\int {\frac{2dx}{ 3 + \cos 2x } \, = -2\int {\frac{dx}{ 3 + \cos 2x } \, =$

Универсальная тригонометрическая подстановка

$\rm tg \ x = t \Longrightarrow \boxed{\rm t^{2} = tg^{2} x }$

$\rm \cos 2x = \dfrac{\rm 1 - tg^{2} x}{\rm 1 + tg^{2} x} = \dfrac{\rm 1 - t^{2}}{\rm 1 + t^{2}}$

$\rm \dfrac{d}{dx} (tg \ x) = \dfrac{1}{\cos^{2} x}$

$\rm \displaystyle dt = d(tg \ x)\ dx \Longrightarrow dx = \frac{dt}{d(tg \ x)} = \frac{dt}{\cfrac{1}{\cos^{2} x} } = \frac{dt}{1 + tg^{2} x} = \frac{dt}{1 + t^{2}}$

$\displaystyle \rm -2\int {\frac{dx}{ 3 + \cos 2x } \, = -2\int {\frac{\cfrac{dt}{1 + t^{2}} }{3+ \cfrac{1 - t^{2}}{1 + t^{2}} } \, = -2\int {\frac{\cfrac{dt}{1 + t^{2}} }{ \cfrac{3(1 + t^{2}) + 1 - t^{2}}{1 + t^{2}} } \, =$

$\displaystyle \rm = -2\int {\frac{dt(1 + t^{2})}{ (3 + 3t^{2} + 1 - t^{2})(1 + t^{2}) } \, = -2\int {\frac{dt}{ (2t^{2} + 4) } = -\frac{2}{2} \int {\frac{dt}{ t^{2} + 2 }=$

$\displaystyle \rm= - \int {\frac{dt}{ t^{2} + (\sqrt{2})^{2} } = - \frac{1}{\sqrt{2} } \ arctg \bigg(\dfrac{t}{\sqrt{2} } \bigg) + C = -\dfrac{\ arctg \bigg(\dfrac{t}{\sqrt{2} } \bigg)}{\sqrt{2} } + C =$

$\displaystyle \rm -\dfrac{\ arctg \bigg(\dfrac{tg \ x}{\sqrt{2} } \bigg)}{\sqrt{2} } + C;$

eefa29549675f14175bda419207898ed.docx