Question

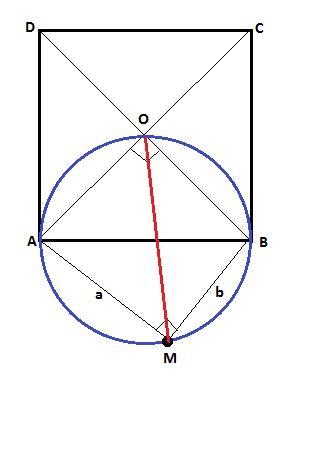
Дан квадрат ABCD с центром в точке O. Вне его выбрана точка M такая, что /_AMB = 90°, AM = 8√2, BM = 7√2. Найдите MO.

Answer 1

Ответ:

15 см

Объяснение:

Смотрите рисунок.

У окружности есть такое свойство: вписанный угол, равный 90°, опирается на диаметр.

Это значит, что существует окружность, для которой AB - диаметр, и на ней лежит и точка О (∠AOB = 90°) и точка M (∠AMB = 90°).

Я эту окружность нарисовал синим.

По условию AM = a = 8√2 см; BM = b = 7√2 см.

По теореме Пифагора:

AB^2 = AM^2 + BM^2 = 64*2 + 49*2 = 128 + 98 = 226

Диаметр круга, он же сторона квадрата:

D = AB = √226 см.

Диагональ квадрата:

d = AC = AB*√2 = √226*√2 = √452 = 2√113 см.

AO = BO = d/2 = 2√113/2 = √113 см.

Найдём углы BAM и OAM:

$cos(BAM)=\frac{AM}{AB} =\frac{8\sqrt{2} }{\sqrt{226} }=\frac{8\sqrt{2} }{\sqrt{2}*\sqrt{113} } =\frac{8}{\sqrt{113} }$

$sin(BAM)=\sqrt{1-cos^2(BAM)} =\sqrt{1-\frac{64}{113} } =\sqrt{\frac{49}{113} } =\frac{7}{\sqrt{113} }$

∠OAB = 45° = π/4

$cos(OAM)=cos(OAB+BAM)=cos(\frac{\pi }{4} +BAM)=$

$=cos(\frac{\pi }{4} )*cos(BAM)-sin(\frac{\pi }{4} )*sin(BAM)=$

$=\frac{1}{\sqrt{2} }*\frac{8}{\sqrt{113} } -\frac{1}{\sqrt{2} } *\frac{7}{\sqrt{113} } =\frac{1}{\sqrt{2} }(\frac{8}{\sqrt{113}}-\frac{7}{\sqrt{113}} )= \frac{1}{\sqrt{2} }*\frac{1}{\sqrt{113} } =\frac{1}{\sqrt{226} }$

Итак, мы получили треугольник AOM, в котором:

AO = √113 см, AM = 8√2 см, cos (OAM) = 1/√226

По теореме косинусов:

MO^2 = AO^2 + AM^2 - 2*AO*AM*cos (OAM) =

= 113 + 64*2 - 2*√113*8√2*1/√226 = 113 + 128 - 2*8*√226/√226 =

= 241 - 16 = 225

MO = √225 = 15 см