В треугольнике MNP угол ∠M равен 90°, а угол ∠N равен 70°, MD – биссектриса. Найдите углы треугольника PDM
Аноним:
ПОМОГИТЕ
Сначала угол Р=90-70=20 . Теперь угол PMD=45 , тк биссектриса разделила угол 90 градусов на два равных. Теперь
угол PDM=180-45-20=........посчитаешь сам?
Чертеж стандартный.
Ответы
Ответ дал:
2
Объяснение:
< NMD=<DMP=90:2=45 градусов, т. к МD - биссектриса.
Тр-к NMD:
<NDM=180-<NMD-<N=180-45-70=65 градусов
Тр-к МDP:
<MDP=180-<NDM=180-65=115 градусов
<DPM=180-<MDP-<DMP=180-115-45=20 градусов
Ответ : <DMP=45 градусов ;
<МDP=115 градусов ; <DPM=20 градусов
Приложения:
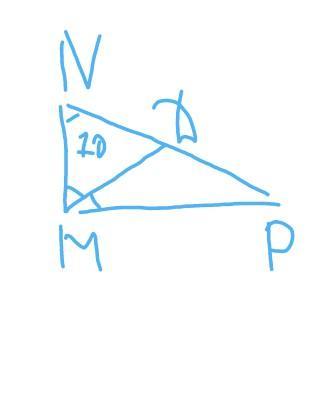
но чертеж ......даже знаю как его назвать....
Вас заинтересует
2 года назад
2 года назад