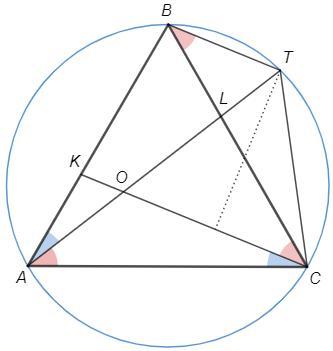
Даю 80 баллов! На сторонах AB и BC равностороннего треугольника ABC взяты точки K и L такие, что AK=BL. Отрезки CK и AL пересекаются в точке O. Серединный перпендикуляр к отрезку CO пересекает прямую AO в точке T. Докажите, что прямые BT и CO параллельны. (с рисунком, если есть возможность)
Ответы
Ответ дал:
1
Треугольники CAK и ABL равны по двум сторонам и углу между ними.
∠ACK=∠BAL => ∠BCK=∠CAL
Сумма синего и красного углов 60°.
Тогда внешний угол COT треугольника AOC равен 60°.
Точка T на серединном перпендикуляре, равноудалена от концов отрезка CO, TC=TO
△CTO - равнобедренный с углом 60° => равносторонний, ∠CTO=60°
Отрезок AC виден из точек B и T под равным углом - точки A-B-T-C на одной окружности.
∠CBT=∠CAT (вписанные, опирающиеся на одну дугу) => ∠CBT=∠BCK
Накрест лежащие углы равны - прямые BT и CK параллельны.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад