Question

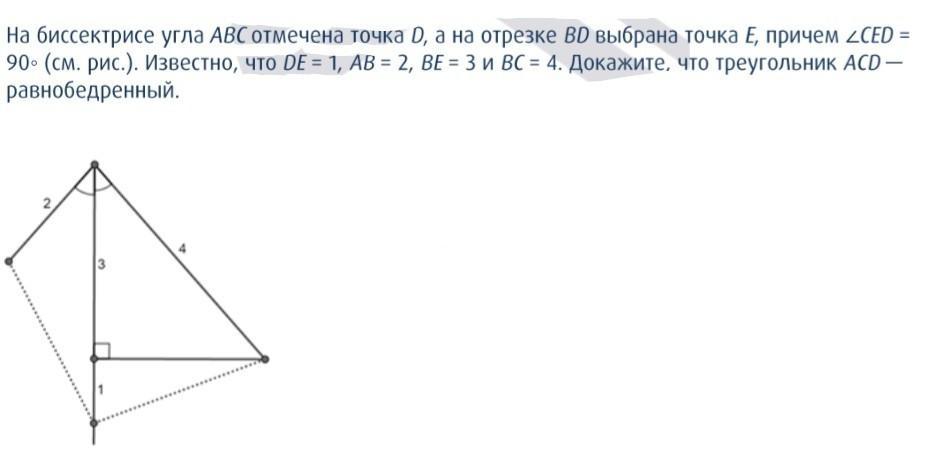
На биссектрисе угла ABC отмечена точка D, а на отрезке BD выбрана точка E, причем угол CED = 90° (см. рис.). Известно, что DE = 1, AB = 2, BE = 3 и ВС = 4. Докажите, что треугольник ACD — равнобедренный​

Answer 1

Отметим на отрезке BE точку F так, что F E = 1, тогда BF = 2. Треугольники ABD и F BC

равны по первому признаку: AB = BF = 2, BD = BC = 4, ∠ABD = ∠F BC. Следовательно, AD = F C.

Далее, отрезок CE является медианой и высотой в треугольнике CDF. Значит, D = F. Таким образом,

AD = DC, что и требовалось.