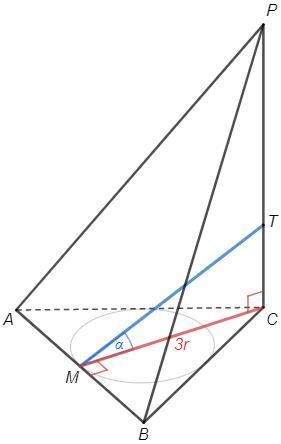
В основании пирамиды лежит правильный треугольник с радиусом вписанной окружности r. Две боковые грани пирамиды перпендикулярны плоскости основания. Некоторая точка высоты пирамиды равноудалена от ее вершины и стороны основания, принадлежащей третьей боковой грани. С данной точки до середины этой стороны произведен отрезок, образующий с плоскостью основания угол α. Определить объем пирамиды.
Ответы
V =1/3 Sосн H
Правильный треугольник ABC дан через радиус вписанной окружности.
Высота треугольника CM=3r
S=3√3 r^2
Знаем площадь основания, осталось найти высоту пирамиды.
Две боковые грани перпендикулярны основанию, следовательно обе проходят через перпендикуляр к основанию, т.е. высоту. Так как две несовпадающие плоскости могут иметь лишь одну общую прямую, боковое ребро PC и есть высота пирамиды, PC⊥(ABC).
По теореме о трех перпендикулярах TM⊥AB. По условию PT=TM. (Расстояние от точки до прямой - длина перпендикуляра.)
Высота CM также является медианой, M - середина AB. По условию ∠TMC=a. (Угол между прямой и плоскостью - угол между прямой и ее проекцией.)
Рассмотрим треугольник TMC.
TC =CM tga =3r tga
TM =CM/cosa =3r/cosa =PT
PC =PT+TC =3r (tga +1/cosa) = 3r(sina +1)/cosa
V = 3√3 r^3 (sina +1)/cosa