Question

Найдите вероятность того, что случайно выбранный из первых 184 натуральных чисел будет кратным 4 трехзначным числом.



А) 11 / 92.

B) 1 / 184.

C) 5 / 11.

D) 5 / 23.

E) 13 / 92.​

Answer 1

Число делится на 4, если две последние его цифры — нули или образуют число, которое делится на 4. У нас таких от 1 до 184 двадцать два трехзначных числа. ( 100; 104, 108, 112, 116, 120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160, 164, 168, 172, 176, 180, 184), чтобы найти  вероятность того, что случайно выбранный из первых 184 натуральных чисел будет кратным 4  трехзначным числом. надо число благоприятствующих исходов, а их m=22, разделить на общее число исходов, а их n=184- по классическому определению вероятности это отношение равно m/n=22/184=11/92

Ответ А) 11/92.

Answer 2

   Если хотите решать такие задания быстро, используйте эти формулы  

Перевод:

Qeyd - Заметка

Yaxud - или

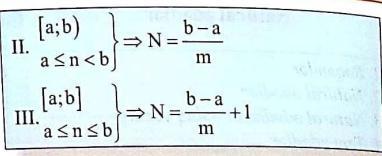
Первая таблица:

Кол — во целых чисел между целыми числами a и  b

Вторая таблица:

Кол — во целых чисел между целыми числами a и  b, делящихся на m

* Для второй таблицы поправка: В конце необходимо найти целую часть.

   Всего чисел (благоприятных случаев):

$\frac{184 - 100}{4} + 1 = 22$

   Согласно классическому определению вероятности:

$p = \frac{22}{184} = \frac{11}{92}$

А)

   Достаточно проверить справедливость формул для случая [a;b)

   Докажем логически.

   Очевидно, что в промежутках [a;b) и [a+1;b+1) одинаковое кол-во чисел. Тогда:

$b-a=(b+1)-(a+1)$

   Это тождество выполняется всегда. QED

Чтобы убедится в справедливости формул во второй таблицы приведём пример:

Сколько целых чисел, делящихся на 25 в промежутке [1;100)?

n({25;50;75}) = 3

А по формуле:

$[\frac{100-1}{25} ] = 3$