Question

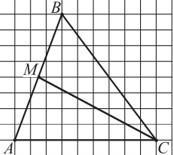
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC с вершинами в узлах сетки (см. рисунок). Найдите длину его медианы СМ

Answer 1

Ответ:

Длина медианы МС равна 8,5 ед.

Объяснение:

На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC с вершинами в узлах сетки (см. рисунок). Найдите длину его медианы СМ.

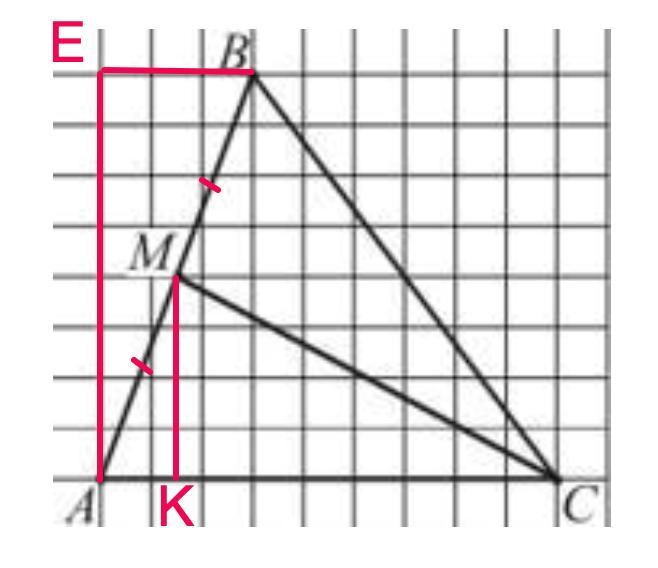
Дополнительное построение.

Из точки М опустим перпендикуляр МК на сторону АС. Построим прямоугольный треугольник АЕВ с гипотенузой АВ.

Из прямоугольного ΔАЕВ по теореме Пифагора найдем гипотенузу.

ЕВ = 3 ед.; АЕ = 8 ед. ⇒

АВ² = АЕ² + ЕВ² = 64 + 9 = 73

АВ = √73 (ед.)

Так СМ - медиана, то

$\displaystyle AM=\frac{\sqrt{73} }{2}$

Из прямоугольного ΔАМК по теореме Пифагора найдем катет АК.

МК = 4 (ед.)

$\displaystyle AK^2=AM^2-MK^2=\frac{73}{4}-16=\frac{73-64}{4}=\frac{9}{4}\\ \\ AK=\sqrt{\frac{9}{4} } =\frac{3}{2}$

АС = 9 ед. Можем найти КС.

$\displaystyle KC=AC-AK=9-\frac{3}{2}=\frac{18-3}{2} =\frac{15}{2}$

Теперь из прямоугольного ΔКМС можем найти МС по теореме Пифагора.

МС² = МК²+ КС²

$\displaystyle MC^2=16+\frac{225}{4}=\frac{64+225}{4} =\frac{289}{4}\\ \\MC=\sqrt{\frac{289}{4} } =\frac{17}{2}=8,5$

Длина медианы МС равна 8,5 ед.