Пожалуйста, помогите решить задание по алгебре (тригонометрия)
Задание на фотографии
Приложения:
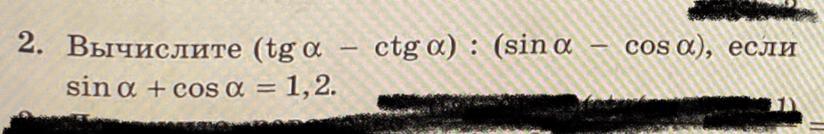
Ответы
Ответ дал:
1
Ответ:
Объяснение: Заметим сначала, что из условия
Поэтому
Замечание. Мы воспользовались основным тригонометрическим тождеством
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад