Ответы
Ответ дал:
6
Ответ:
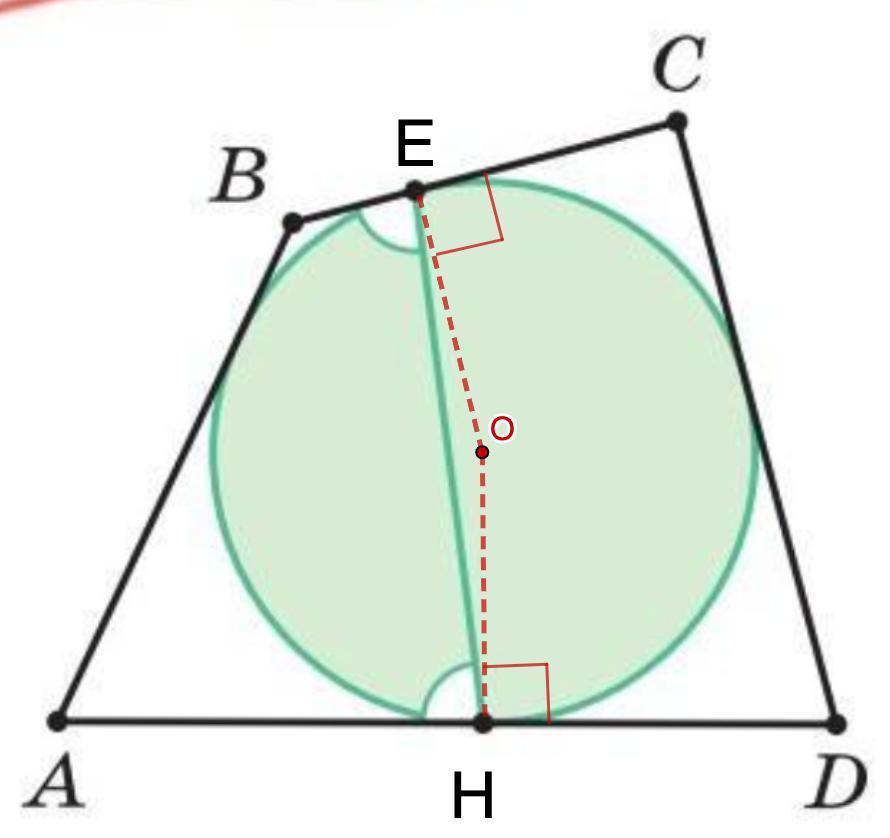
Доказано, что хорда, которая соединяет точки ее касания с противоположными сторонами этого четырехугольника, образует с этими сторонами равные углы.
∠ВЕН = ∠ЕНА.
Объяснение:
Требуется доказать, что хорда, которая соединяет точки ее касания с противоположными сторонами этого четырехугольника, образует с этими сторонами равные углы.
Дано: ABCD - четырехугольник;
Окр.О - вписанная;
Доказать: ∠ВЕН = ∠ЕНА.
Доказательство:
1.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ∠ВЕО = ∠ОНА = 90°
2. Рассмотрим ΔЕОН.
ОЕ = ОН = R
⇒ ΔЕОН - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠ОЕН = ∠ОНЕ
3. ∠ВЕН = ∠ВЕО - ∠ОЕН = 90° - ∠ОЕН
∠ЕНА = ∠ОНА - ∠ОНЕ = 90° - ∠ОНЕ
⇒ ∠ВЕН = ∠ЕНА
Что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
