На продолжении стороны AC треугольника ABC взяли точки K и E так, что AK = BC, CE = AB. Докажите, что центр вписанной в треугольник ABC окружности равноудалён от точек K и E
Приложения:

Ответы
Ответ дал:
6
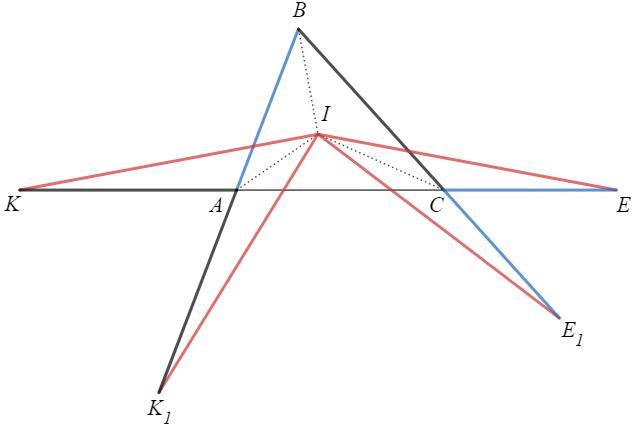
На продолжениях AB и BC отметим точки K1 и E1
AK1=AK=BC, CE1=CE=AB
=> BK1=BE1
Центр вписанной окружности - точка пересечения биссектрис (I).
Стороны угла симметричны относительно его биссектрисы. Точки K и K1 симметричны относительно биссектрисы угла A. Тогда IK=IK1.
Аналогично IE=IE1.
Точки K1 и E1 симметричны относительно биссектрисы угла B, IK1=IE1.
=> IK=IK1=IE1=IE
То же самое через равенство треугольников: △IAK=△IAK1 по двум сторонам и углу между ними и т.д.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад