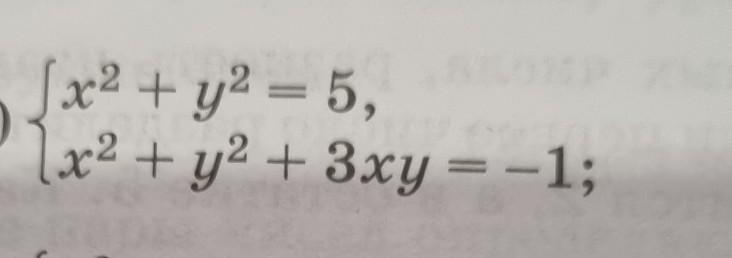Ответы
Ответ дал:
1
Ответ:
( 2 ; -1 ) , (-2 ; 1 ) , ( 1 ; -2 ) , (-1 ; 2 )
Объяснение:
1 = 1·1
1=(-1)·(-1)
9 = 3·3
9 = (-3)·(-3)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад