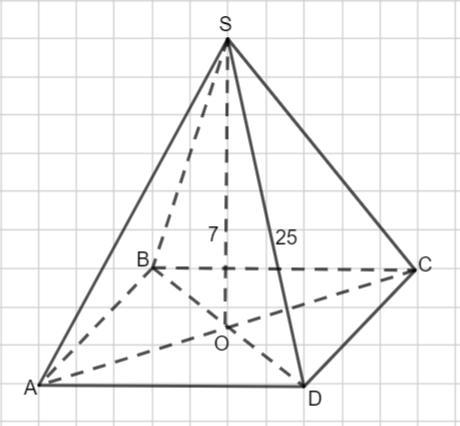
В правильный четырехугольной пирамиде SABCD точка O - центр основания, S - вершина, SO=7, SD=25. Найдите длину отрезка BD.
Ответы
Ответ дал:
1
Ответ:
Длина отрезка BD равна 48.
Объяснение:
По условию задана правильна четырехугольная пирамида
SABCD .
Точка О- центр основания. S- вершина, SO= 7, SD=25.
SO - высота пирамиды. Рассмотрим Δ SOD - прямоугольный и применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В основании правильной четырехугольной призмы квадрат. Диагонали квадрата пересекаясь, делятся пополам.
Тогда диагональ
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад