Question

все на фото,геометрия​

Answer 1

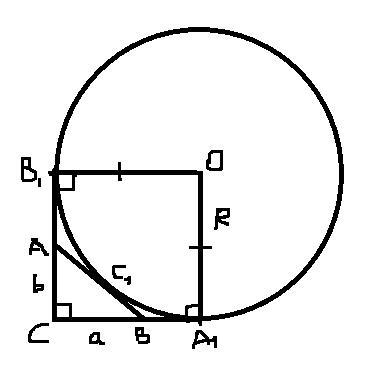
Пусть вершины треугольника: A, B, C, и a = BC, c = AB (угол C - прямой),  b = AC (см. рис.) Пусть О - центр получившейся окружности с искомым радиусом R, а A1, B1, C1 - точки касания с прямыми BC, AC, AB соответственно (см. рис.)

Проведя радиусы OA1 и OB1, получаем четырёхугольник OB1CA1 с 2-мя равными сторонам (OB1 и OA1) и 3-мя прямыми углами (∠C - прямой по условию, ∠OB1C = ∠OA1C = 90° как угол между касательной и радиусом в точке касания). Значит OB1CA1 - квадрат со стороной R.

Поэтому A1C = R, BC1 = BA1 = R - a (равны как отрезки пересекающихся касательных), AB1 = AC1 = R - b (аналогично).

c = AB = AC1 + BC1 = R - b + R - a = 2R - a - b, откуда $R = \frac{a+b+c}{2}$

Решив уравнение $\frac{a+b+c}{2} = \frac{ab}{a+b-c}$, получаем, что оно верно для любых положительных a и b, то есть для любого прям. треугольника с катетами a, b ($c=\sqrt{a^2+b^2}$)

Решение уравнения:

$\frac{a + b + c}{2} = \frac{ab}{a+b-c}\\ ((a+b) + c)((a+b)-c) = 2ab\\(a+b)^2 - c^2 = 2ab\\a^2 + b^2 + 2ab - a^2 - b^2 = 2ab\\2ab = 2ab$