Знайдіть косинус кута між векторами a і b, якщо a=2m+3n b=3m-n |m|= |n|=1 , і m та n перпендикулярні. Даю 100 баллов!
Приложения:
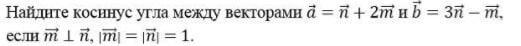
orjabinina:
Ваши записи не соответствуют прикрепленному скрину. Где верно?
Если можете, то лучше решайте то, что я написал в своих записах
Ответы
Ответ дал:
5
Найдите косинус угла между векторами a и b, если a=2m+3n ,b=3m-n ,|m|= |n|=1 и вектора m и n перпендикулярны.
Объяснение:
1)
2) =
Скалярный квадрат ,
Скалярный квадрат .
Скалярное произведение векторов равно нулю , тк они перпендикулярны. Тогда
.
3) Длины векторов -это длины отрезков на которых лежат эти вектора . По условию вектора перпендикулярны .
a) Суммой векторов (чертеж 1) по правилу параллелограмма будет вектор
. Длину найдем из прямоугольного ΔАСК с длиной катетов 2 и 3 по теореме Пифагора
.
б) Разностью векторов (чертеж 2) будет вектор
.Из ΔАВС-прямоугольного , по т. Пифагора
4)
.
Приложения:

Спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад